Micro-Browsing Models for Search Snippets

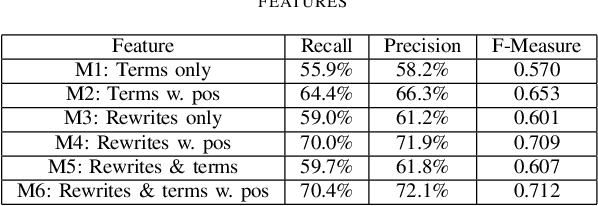
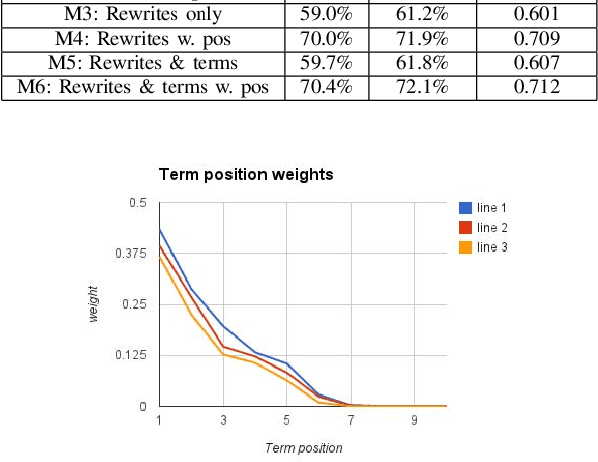
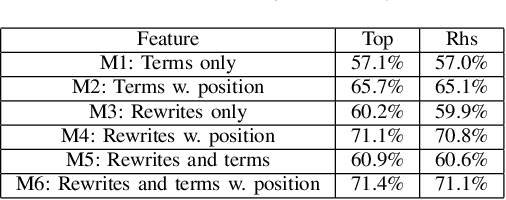
Click-through rate (CTR) is a key signal of relevance for search engine results, both organic and sponsored. CTR of a result has two core components: (a) the probability of examination of a result by a user, and (b) the perceived relevance of the result given that it has been examined by the user. There has been considerable work on user browsing models, to model and analyze both the examination and the relevance components of CTR. In this paper, we propose a novel formulation: a micro-browsing model for how users read result snippets. The snippet text of a result often plays a critical role in the perceived relevance of the result. We study how particular words within a line of snippet can influence user behavior. We validate this new micro-browsing user model by considering the problem of predicting which snippet will yield higher CTR, and show that classification accuracy is dramatically higher with our micro-browsing user model. The key insight in this paper is that varying relatively few words within a snippet, and even their location within a snippet, can have a significant influence on the clickthrough of a snippet.

Inference in Probabilistic Logic Programs with Continuous Random Variables

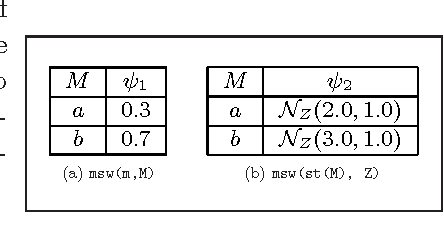
Probabilistic Logic Programming (PLP), exemplified by Sato and Kameya's PRISM, Poole's ICL, Raedt et al's ProbLog and Vennekens et al's LPAD, is aimed at combining statistical and logical knowledge representation and inference. A key characteristic of PLP frameworks is that they are conservative extensions to non-probabilistic logic programs which have been widely used for knowledge representation. PLP frameworks extend traditional logic programming semantics to a distribution semantics, where the semantics of a probabilistic logic program is given in terms of a distribution over possible models of the program. However, the inference techniques used in these works rely on enumerating sets of explanations for a query answer. Consequently, these languages permit very limited use of random variables with continuous distributions. In this paper, we present a symbolic inference procedure that uses constraints and represents sets of explanations without enumeration. This permits us to reason over PLPs with Gaussian or Gamma-distributed random variables (in addition to discrete-valued random variables) and linear equality constraints over reals. We develop the inference procedure in the context of PRISM; however the procedure's core ideas can be easily applied to other PLP languages as well. An interesting aspect of our inference procedure is that PRISM's query evaluation process becomes a special case in the absence of any continuous random variables in the program. The symbolic inference procedure enables us to reason over complex probabilistic models such as Kalman filters and a large subclass of Hybrid Bayesian networks that were hitherto not possible in PLP frameworks. (To appear in Theory and Practice of Logic Programming).

Parameter Learning in PRISM Programs with Continuous Random Variables

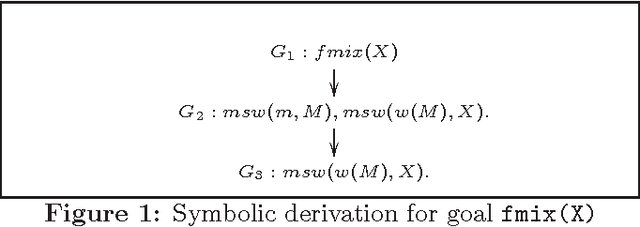
Probabilistic Logic Programming (PLP), exemplified by Sato and Kameya's PRISM, Poole's ICL, De Raedt et al's ProbLog and Vennekens et al's LPAD, combines statistical and logical knowledge representation and inference. Inference in these languages is based on enumerative construction of proofs over logic programs. Consequently, these languages permit very limited use of random variables with continuous distributions. In this paper, we extend PRISM with Gaussian random variables and linear equality constraints, and consider the problem of parameter learning in the extended language. Many statistical models such as finite mixture models and Kalman filter can be encoded in extended PRISM. Our EM-based learning algorithm uses a symbolic inference procedure that represents sets of derivations without enumeration. This permits us to learn the distribution parameters of extended PRISM programs with discrete as well as Gaussian variables. The learning algorithm naturally generalizes the ones used for PRISM and Hybrid Bayesian Networks.