Parameter Learning in PRISM Programs with Continuous Random Variables
Paper and Code
Mar 19, 2012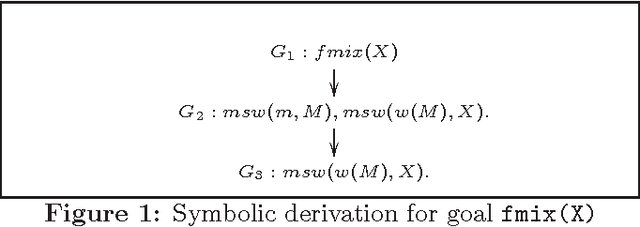
Probabilistic Logic Programming (PLP), exemplified by Sato and Kameya's PRISM, Poole's ICL, De Raedt et al's ProbLog and Vennekens et al's LPAD, combines statistical and logical knowledge representation and inference. Inference in these languages is based on enumerative construction of proofs over logic programs. Consequently, these languages permit very limited use of random variables with continuous distributions. In this paper, we extend PRISM with Gaussian random variables and linear equality constraints, and consider the problem of parameter learning in the extended language. Many statistical models such as finite mixture models and Kalman filter can be encoded in extended PRISM. Our EM-based learning algorithm uses a symbolic inference procedure that represents sets of derivations without enumeration. This permits us to learn the distribution parameters of extended PRISM programs with discrete as well as Gaussian variables. The learning algorithm naturally generalizes the ones used for PRISM and Hybrid Bayesian Networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge