Inference in Probabilistic Logic Programs using Lifted Explanations
Paper and Code
Aug 20, 2016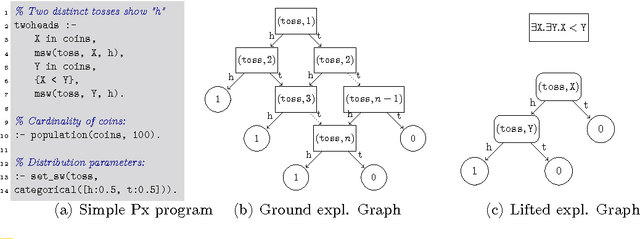
In this paper, we consider the problem of lifted inference in the context of Prism-like probabilistic logic programming languages. Traditional inference in such languages involves the construction of an explanation graph for the query and computing probabilities over this graph. When evaluating queries over probabilistic logic programs with a large number of instances of random variables, traditional methods treat each instance separately. For many programs and queries, we observe that explanations can be summarized into substantially more compact structures, which we call lifted explanation graphs. In this paper, we define lifted explanation graphs and operations over them. In contrast to existing lifted inference techniques, our method for constructing lifted explanations naturally generalizes existing methods for constructing explanation graphs. To compute probability of query answers, we solve recurrences generated from the lifted graphs. We show examples where the use of our technique reduces the asymptotic complexity of inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge