FedRand: Enhancing Privacy in Federated Learning with Randomized LoRA Subparameter Updates

Federated Learning (FL) is a widely used framework for training models in a decentralized manner, ensuring that the central server does not have direct access to data from local clients. However, this approach may still fail to fully preserve data privacy, as models from local clients are exposed to the central server during the aggregation process. This issue becomes even more critical when training vision-language models (VLMs) with FL, as VLMs can easily memorize training data instances, making them vulnerable to membership inference attacks (MIAs). To address this challenge, we propose the FedRand framework, which avoids disclosing the full set of client parameters. In this framework, each client randomly selects subparameters of Low-Rank Adaptation (LoRA) from the server and keeps the remaining counterparts of the LoRA weights as private parameters. After training both parameters on the client's private dataset, only the non-private client parameters are sent back to the server for aggregation. This approach mitigates the risk of exposing client-side VLM parameters, thereby enhancing data privacy. We empirically validate that FedRand improves robustness against MIAs compared to relevant baselines while achieving accuracy comparable to methods that communicate full LoRA parameters across several benchmark datasets.

Cost-Sensitive Multi-Fidelity Bayesian Optimization with Transfer of Learning Curve Extrapolation

In this paper, we address the problem of cost-sensitive multi-fidelity Bayesian Optimization (BO) for efficient hyperparameter optimization (HPO). Specifically, we assume a scenario where users want to early-stop the BO when the performance improvement is not satisfactory with respect to the required computational cost. Motivated by this scenario, we introduce utility, which is a function predefined by each user and describes the trade-off between cost and performance of BO. This utility function, combined with our novel acquisition function and stopping criterion, allows us to dynamically choose for each BO step the best configuration that we expect to maximally improve the utility in future, and also automatically stop the BO around the maximum utility. Further, we improve the sample efficiency of existing learning curve (LC) extrapolation methods with transfer learning, while successfully capturing the correlations between different configurations to develop a sensible surrogate function for multi-fidelity BO. We validate our algorithm on various LC datasets and found it outperform all the previous multi-fidelity BO and transfer-BO baselines we consider, achieving significantly better trade-off between cost and performance of BO.

Robust Neural Networks inspired by Strong Stability Preserving Runge-Kutta methods

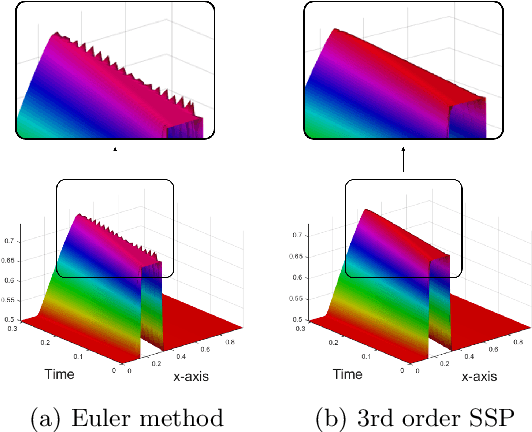
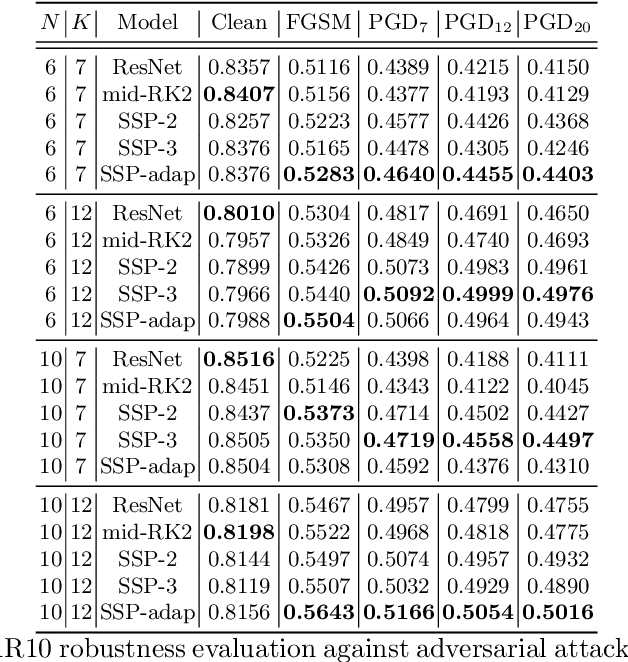
Deep neural networks have achieved state-of-the-art performance in a variety of fields. Recent works observe that a class of widely used neural networks can be viewed as the Euler method of numerical discretization. From the numerical discretization perspective, Strong Stability Preserving (SSP) methods are more advanced techniques than the explicit Euler method that produce both accurate and stable solutions. Motivated by the SSP property and a generalized Runge-Kutta method, we propose Strong Stability Preserving networks (SSP networks) which improve robustness against adversarial attacks. We empirically demonstrate that the proposed networks improve the robustness against adversarial examples without any defensive methods. Further, the SSP networks are complementary with a state-of-the-art adversarial training scheme. Lastly, our experiments show that SSP networks suppress the blow-up of adversarial perturbations. Our results open up a way to study robust architectures of neural networks leveraging rich knowledge from numerical discretization literature.