Deep neural network for solving differential equations motivated by Legendre-Galerkin approximation

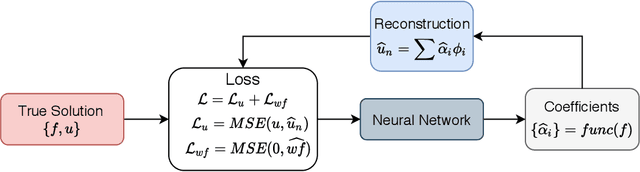
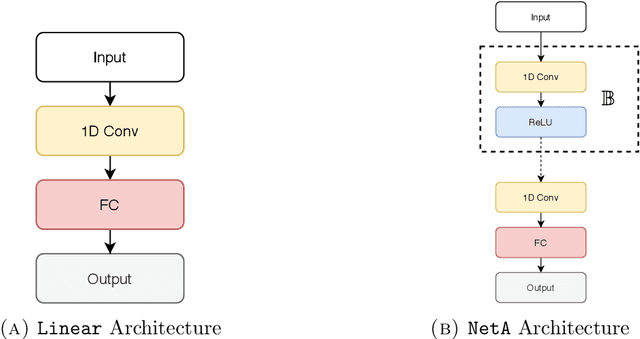
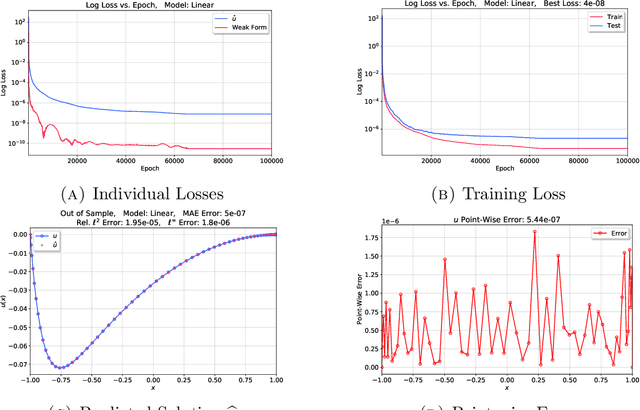
Nonlinear differential equations are challenging to solve numerically and are important to understanding the dynamics of many physical systems. Deep neural networks have been applied to help alleviate the computational cost that is associated with solving these systems. We explore the performance and accuracy of various neural architectures on both linear and nonlinear differential equations by creating accurate training sets with the spectral element method. Next, we implement a novel Legendre-Galerkin Deep Neural Network (LGNet) algorithm to predict solutions to differential equations. By constructing a set of a linear combination of the Legendre basis, we predict the corresponding coefficients, $\alpha_i$ which successfully approximate the solution as a sum of smooth basis functions $u \simeq \sum_{i=0}^{N} \alpha_i \varphi_i$. As a computational example, linear and nonlinear models with Dirichlet or Neumann boundary conditions are considered.

Robust Neural Networks inspired by Strong Stability Preserving Runge-Kutta methods

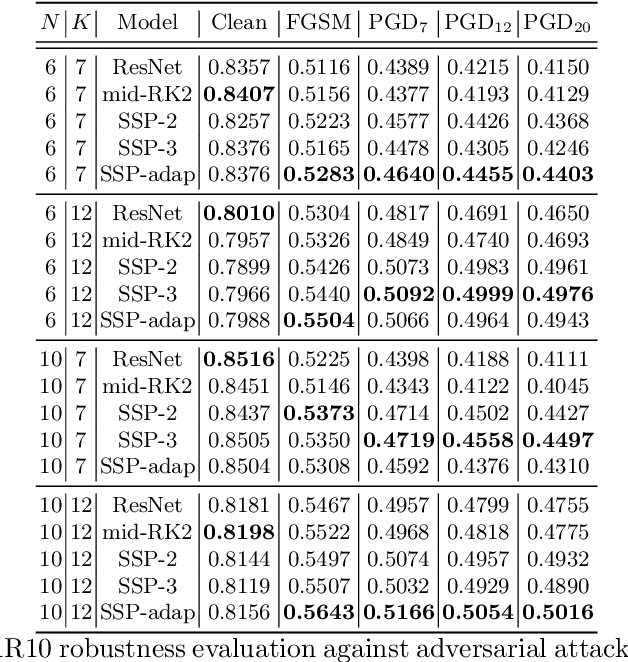
Deep neural networks have achieved state-of-the-art performance in a variety of fields. Recent works observe that a class of widely used neural networks can be viewed as the Euler method of numerical discretization. From the numerical discretization perspective, Strong Stability Preserving (SSP) methods are more advanced techniques than the explicit Euler method that produce both accurate and stable solutions. Motivated by the SSP property and a generalized Runge-Kutta method, we propose Strong Stability Preserving networks (SSP networks) which improve robustness against adversarial attacks. We empirically demonstrate that the proposed networks improve the robustness against adversarial examples without any defensive methods. Further, the SSP networks are complementary with a state-of-the-art adversarial training scheme. Lastly, our experiments show that SSP networks suppress the blow-up of adversarial perturbations. Our results open up a way to study robust architectures of neural networks leveraging rich knowledge from numerical discretization literature.