Robust Neural Networks inspired by Strong Stability Preserving Runge-Kutta methods
Paper and Code
Oct 20, 2020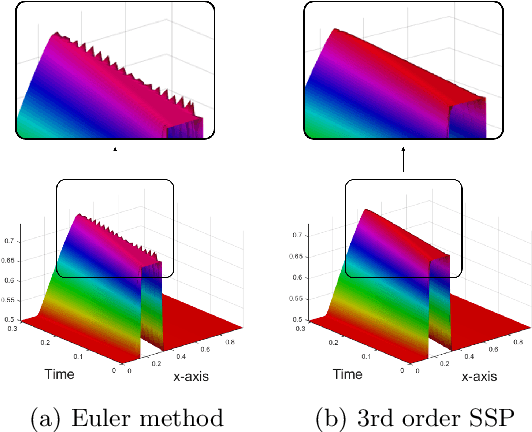

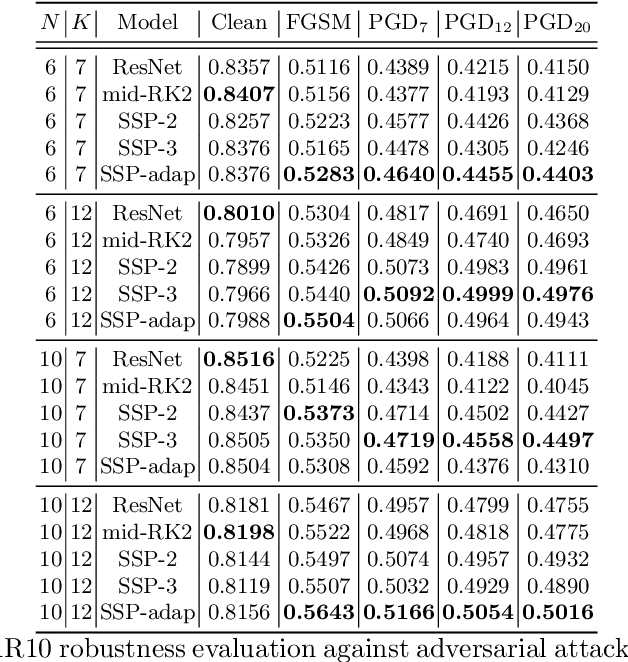

Deep neural networks have achieved state-of-the-art performance in a variety of fields. Recent works observe that a class of widely used neural networks can be viewed as the Euler method of numerical discretization. From the numerical discretization perspective, Strong Stability Preserving (SSP) methods are more advanced techniques than the explicit Euler method that produce both accurate and stable solutions. Motivated by the SSP property and a generalized Runge-Kutta method, we propose Strong Stability Preserving networks (SSP networks) which improve robustness against adversarial attacks. We empirically demonstrate that the proposed networks improve the robustness against adversarial examples without any defensive methods. Further, the SSP networks are complementary with a state-of-the-art adversarial training scheme. Lastly, our experiments show that SSP networks suppress the blow-up of adversarial perturbations. Our results open up a way to study robust architectures of neural networks leveraging rich knowledge from numerical discretization literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge