Deep neural network for solving differential equations motivated by Legendre-Galerkin approximation
Paper and Code
Oct 24, 2020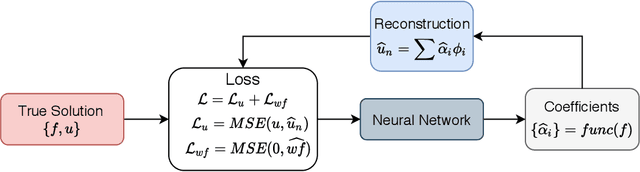
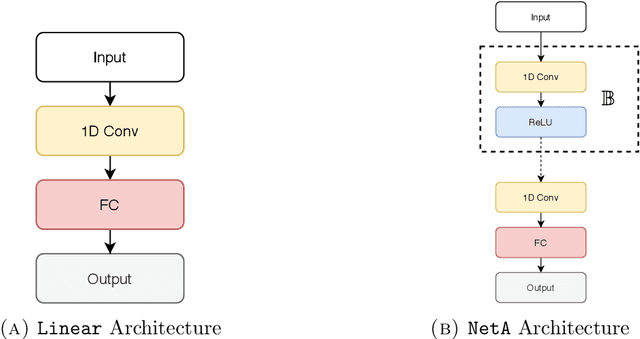
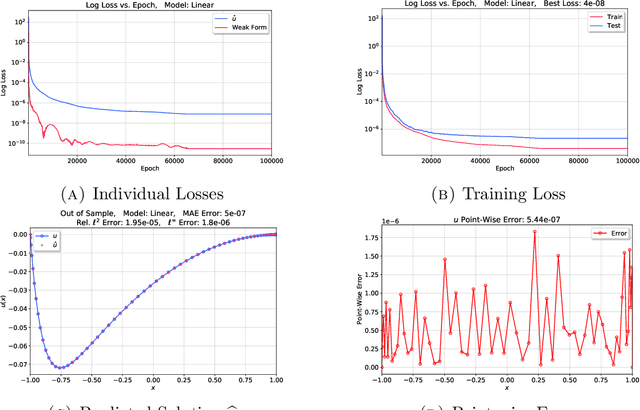

Nonlinear differential equations are challenging to solve numerically and are important to understanding the dynamics of many physical systems. Deep neural networks have been applied to help alleviate the computational cost that is associated with solving these systems. We explore the performance and accuracy of various neural architectures on both linear and nonlinear differential equations by creating accurate training sets with the spectral element method. Next, we implement a novel Legendre-Galerkin Deep Neural Network (LGNet) algorithm to predict solutions to differential equations. By constructing a set of a linear combination of the Legendre basis, we predict the corresponding coefficients, $\alpha_i$ which successfully approximate the solution as a sum of smooth basis functions $u \simeq \sum_{i=0}^{N} \alpha_i \varphi_i$. As a computational example, linear and nonlinear models with Dirichlet or Neumann boundary conditions are considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge