Target-Prompt Online Graph Collaborative Learning for Temporal QoS Prediction

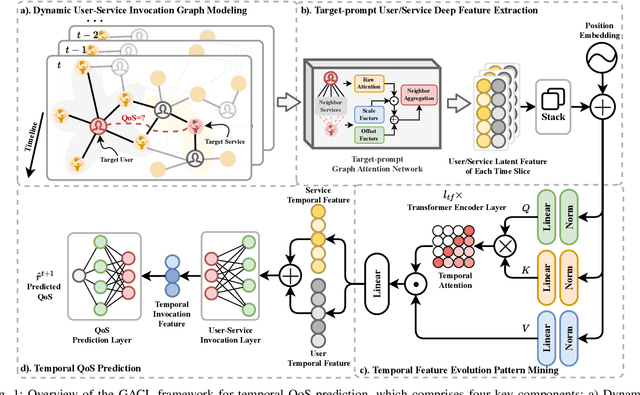
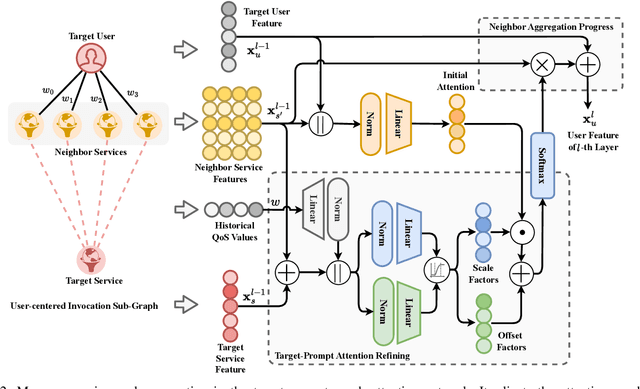
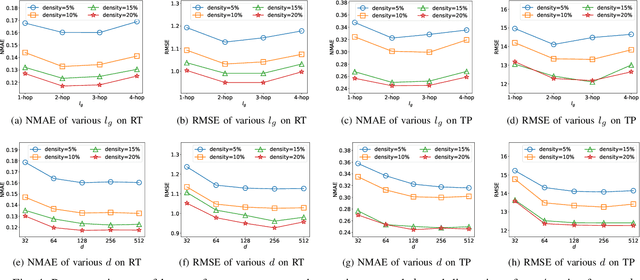
In service-oriented architecture, accurately predicting the Quality of Service (QoS) is vital for maintaining reliability and enhancing user satisfaction. However, current methods often neglect high-order latent collaborative relationships and fail to dynamically adjust feature learning for specific user-service invocations, which are critical for precise feature extraction. Moreover, relying on RNNs to capture QoS evolution limits the ability to detect long-term trends due to challenges in managing long-range dependencies. To address these issues, we propose the Target-Prompt Online Graph Collaborative Learning (TOGCL) framework for temporal QoS prediction. It leverages a dynamic user-service invocation graph to comprehensively model historical interactions. Building on this graph, it develops a target-prompt graph attention network to extract online deep latent features of users and services at each time slice, considering implicit target-neighboring collaborative relationships and historical QoS values. Additionally, a multi-layer Transformer encoder is employed to uncover temporal feature evolution patterns, enhancing temporal QoS prediction. Extensive experiments on the WS-DREAM dataset demonstrate that TOGCL significantly outperforms state-of-the-art methods across multiple metrics, achieving improvements of up to 38.80\%. These results underscore the effectiveness of TOGCL for temporal QoS prediction.

Large Language Model Meets Graph Neural Network in Knowledge Distillation

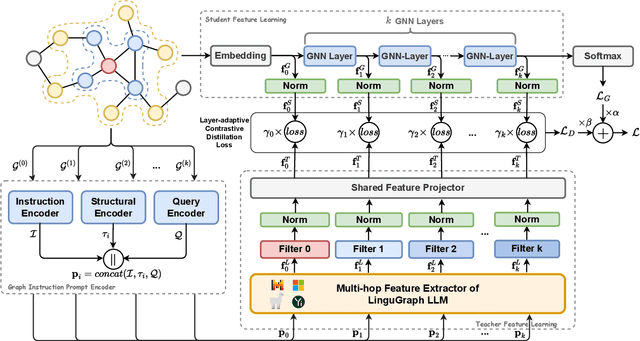
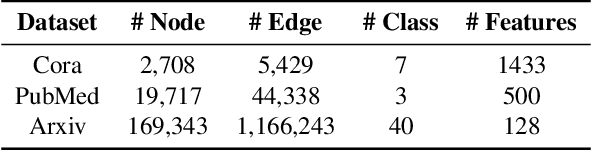
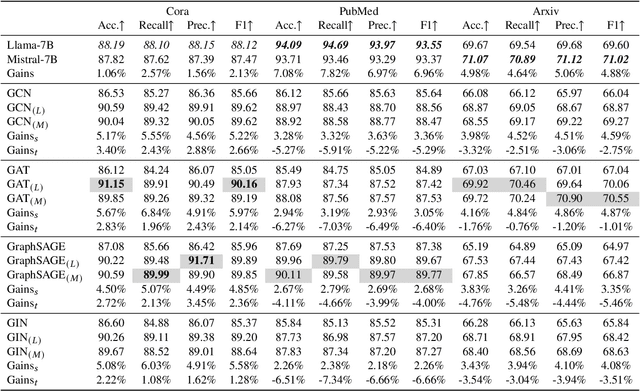
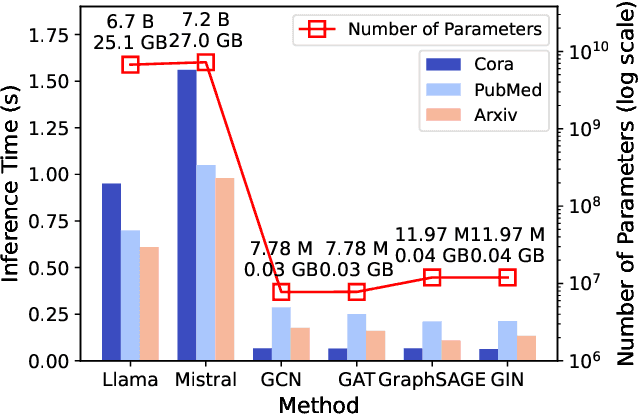
Despite recent community revelations about the advancements and potential applications of Large Language Models (LLMs) in understanding Text-Attributed Graph (TAG), the deployment of LLMs for production is hindered by its high computational and storage requirements, as well as long latencies during model inference. Simultaneously, although traditional Graph Neural Networks (GNNs) are light weight and adept at learning structural features of graphs, their ability to grasp the complex semantics in TAG is somewhat constrained for real applications. To address these limitations, we concentrate on the downstream task of node classification in TAG and propose a novel graph knowledge distillation framework, termed Linguistic Graph Knowledge Distillation (LinguGKD), using LLMs as teacher models and GNNs as student models for knowledge distillation. It involves TAG-oriented instruction tuning of LLM on designed tailored prompts, followed by propagating knowledge and aligning the hierarchically learned node features from the teacher LLM to the student GNN in latent space, employing a layer-adaptive contrastive learning strategy. Through extensive experiments on a variety of LLM and GNN models and multiple benchmark datasets, the proposed LinguGKD significantly boosts the student GNN's predictive accuracy and convergence rate, without the need of extra data or model parameters. Compared to teacher LLM, distilled GNN achieves superior inference speed equipped with much fewer computing and storage demands, when surpassing the teacher LLM's classification accuracy on some of benchmark datasets.

Recurrent Transformer for Dynamic Graph Representation Learning with Edge Temporal States

Dynamic graph representation learning is growing as a trending yet challenging research task owing to the widespread demand for graph data analysis in real world applications. Despite the encouraging performance of many recent works that build upon recurrent neural networks (RNNs) and graph neural networks (GNNs), they fail to explicitly model the impact of edge temporal states on node features over time slices. Additionally, they are challenging to extract global structural features because of the inherent over-smoothing disadvantage of GNNs, which further restricts the performance. In this paper, we propose a recurrent difference graph transformer (RDGT) framework, which firstly assigns the edges in each snapshot with various types and weights to illustrate their specific temporal states explicitly, then a structure-reinforced graph transformer is employed to capture the temporal node representations by a recurrent learning paradigm. Experimental results on four real-world datasets demonstrate the superiority of RDGT for discrete dynamic graph representation learning, as it consistently outperforms competing methods in dynamic link prediction tasks.

Stochastic Primal-Dual Proximal ExtraGradient Descent for Compositely Regularized Optimization

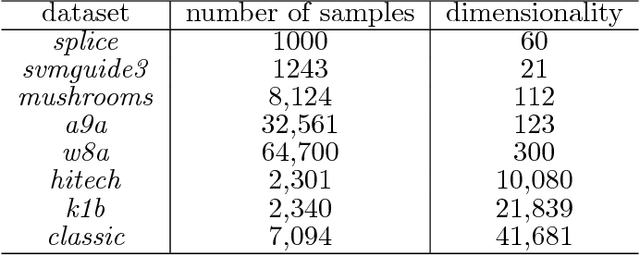
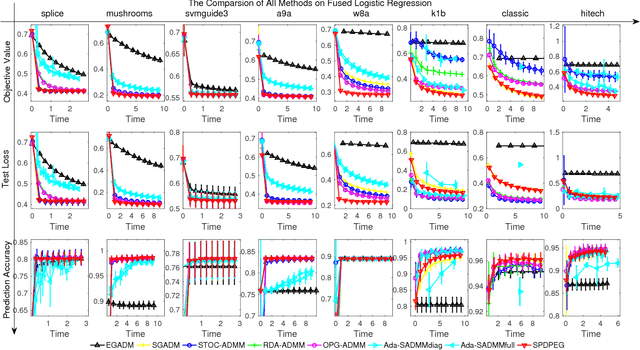
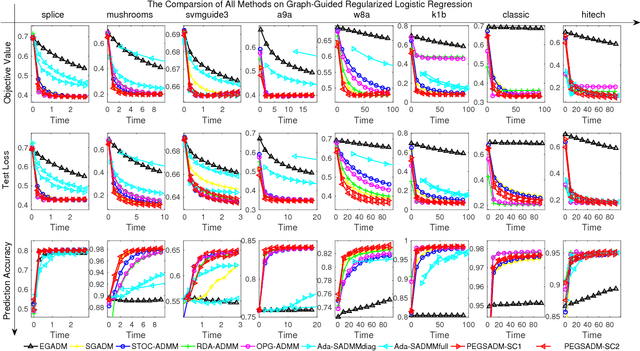
We consider a wide range of regularized stochastic minimization problems with two regularization terms, one of which is composed with a linear function. This optimization model abstracts a number of important applications in artificial intelligence and machine learning, such as fused Lasso, fused logistic regression, and a class of graph-guided regularized minimization. The computational challenges of this model are in two folds. On one hand, the closed-form solution of the proximal mapping associated with the composed regularization term or the expected objective function is not available. On the other hand, the calculation of the full gradient of the expectation in the objective is very expensive when the number of input data samples is considerably large. To address these issues, we propose a stochastic variant of extra-gradient type methods, namely \textsf{Stochastic Primal-Dual Proximal ExtraGradient descent (SPDPEG)}, and analyze its convergence property for both convex and strongly convex objectives. For general convex objectives, the uniformly average iterates generated by \textsf{SPDPEG} converge in expectation with $O(1/\sqrt{t})$ rate. While for strongly convex objectives, the uniformly and non-uniformly average iterates generated by \textsf{SPDPEG} converge with $O(\log(t)/t)$ and $O(1/t)$ rates, respectively. The order of the rate of the proposed algorithm is known to match the best convergence rate for first-order stochastic algorithms. Experiments on fused logistic regression and graph-guided regularized logistic regression problems show that the proposed algorithm performs very efficiently and consistently outperforms other competing algorithms.