Stochastic Primal-Dual Proximal ExtraGradient Descent for Compositely Regularized Optimization
Paper and Code
Feb 01, 2018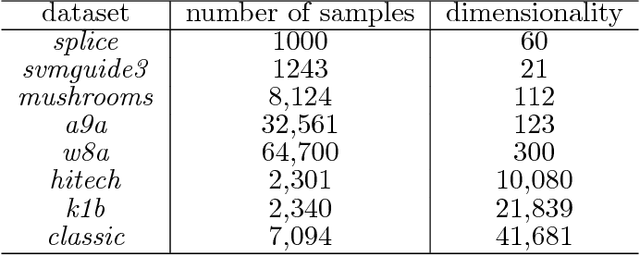
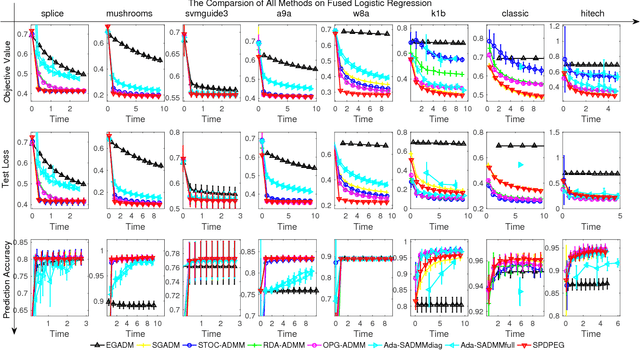
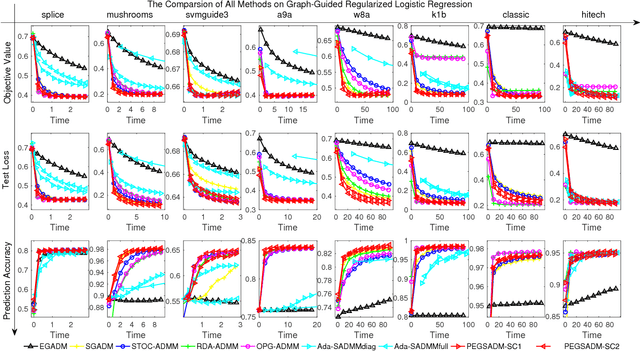
We consider a wide range of regularized stochastic minimization problems with two regularization terms, one of which is composed with a linear function. This optimization model abstracts a number of important applications in artificial intelligence and machine learning, such as fused Lasso, fused logistic regression, and a class of graph-guided regularized minimization. The computational challenges of this model are in two folds. On one hand, the closed-form solution of the proximal mapping associated with the composed regularization term or the expected objective function is not available. On the other hand, the calculation of the full gradient of the expectation in the objective is very expensive when the number of input data samples is considerably large. To address these issues, we propose a stochastic variant of extra-gradient type methods, namely \textsf{Stochastic Primal-Dual Proximal ExtraGradient descent (SPDPEG)}, and analyze its convergence property for both convex and strongly convex objectives. For general convex objectives, the uniformly average iterates generated by \textsf{SPDPEG} converge in expectation with $O(1/\sqrt{t})$ rate. While for strongly convex objectives, the uniformly and non-uniformly average iterates generated by \textsf{SPDPEG} converge with $O(\log(t)/t)$ and $O(1/t)$ rates, respectively. The order of the rate of the proposed algorithm is known to match the best convergence rate for first-order stochastic algorithms. Experiments on fused logistic regression and graph-guided regularized logistic regression problems show that the proposed algorithm performs very efficiently and consistently outperforms other competing algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge