Bindya Venkatesh
Ask-n-Learn: Active Learning via Reliable Gradient Representations for Image Classification
Sep 30, 2020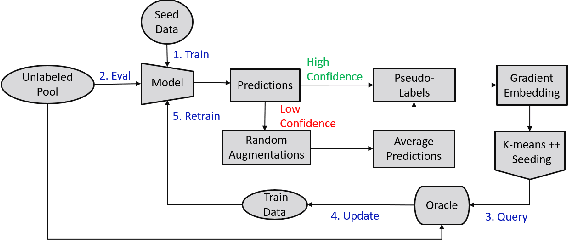
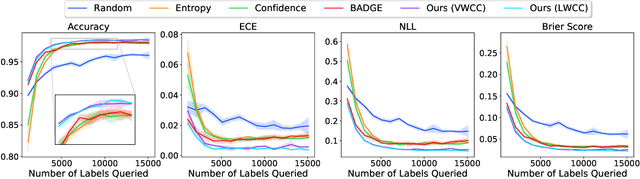
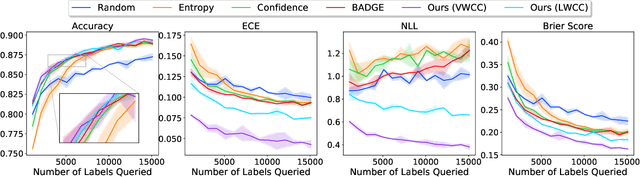
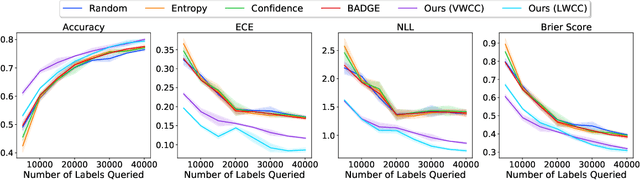
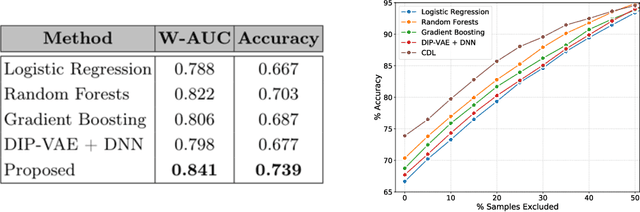
Abstract:Deep predictive models rely on human supervision in the form of labeled training data. Obtaining large amounts of annotated training data can be expensive and time consuming, and this becomes a critical bottleneck while building such models in practice. In such scenarios, active learning (AL) strategies are used to achieve faster convergence in terms of labeling efforts. Existing active learning employ a variety of heuristics based on uncertainty and diversity to select query samples. Despite their wide-spread use, in practice, their performance is limited by a number of factors including non-calibrated uncertainties, insufficient trade-off between data exploration and exploitation, presence of confirmation bias etc. In order to address these challenges, we propose Ask-n-Learn, an active learning approach based on gradient embeddings obtained using the pesudo-labels estimated in each iteration of the algorithm. More importantly, we advocate the use of prediction calibration to obtain reliable gradient embeddings, and propose a data augmentation strategy to alleviate the effects of confirmation bias during pseudo-labeling. Through empirical studies on benchmark image classification tasks (CIFAR-10, SVHN, Fashion-MNIST, MNIST), we demonstrate significant improvements over state-of-the-art baselines, including the recently proposed BADGE algorithm.
Designing Accurate Emulators for Scientific Processes using Calibration-Driven Deep Models
May 05, 2020
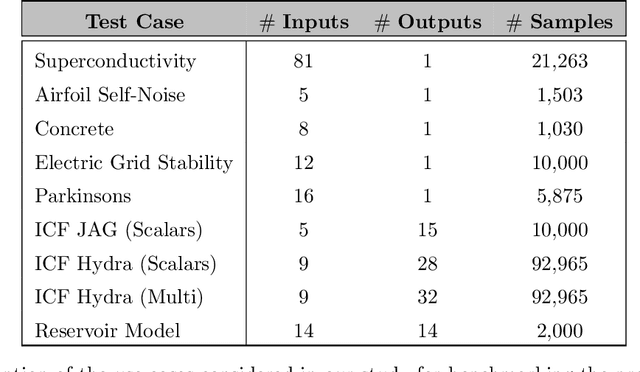

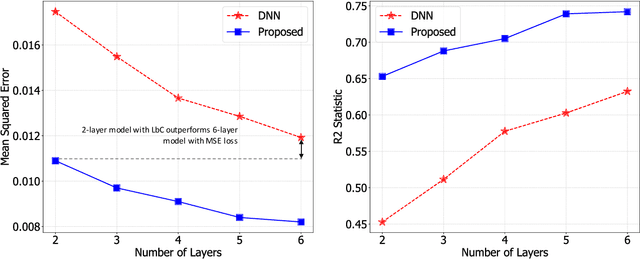
Abstract:Predictive models that accurately emulate complex scientific processes can achieve exponential speed-ups over numerical simulators or experiments, and at the same time provide surrogates for improving the subsequent analysis. Consequently, there is a recent surge in utilizing modern machine learning (ML) methods, such as deep neural networks, to build data-driven emulators. While the majority of existing efforts has focused on tailoring off-the-shelf ML solutions to better suit the scientific problem at hand, we study an often overlooked, yet important, problem of choosing loss functions to measure the discrepancy between observed data and the predictions from a model. Due to lack of better priors on the expected residual structure, in practice, simple choices such as the mean squared error and the mean absolute error are made. However, the inherent symmetric noise assumption made by these loss functions makes them inappropriate in cases where the data is heterogeneous or when the noise distribution is asymmetric. We propose Learn-by-Calibrating (LbC), a novel deep learning approach based on interval calibration for designing emulators in scientific applications, that are effective even with heterogeneous data and are robust to outliers. Using a large suite of use-cases, we show that LbC provides significant improvements in generalization error over widely-adopted loss function choices, achieves high-quality emulators even in small data regimes and more importantly, recovers the inherent noise structure without any explicit priors.
Calibrating Healthcare AI: Towards Reliable and Interpretable Deep Predictive Models
Apr 27, 2020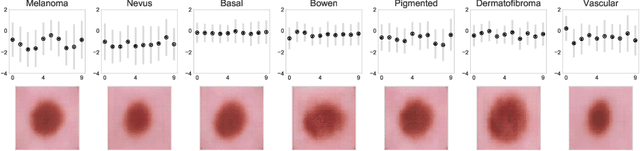
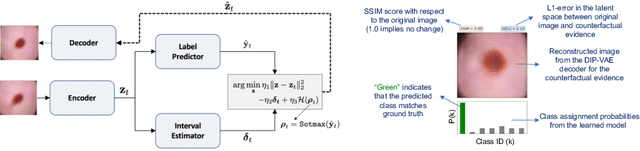
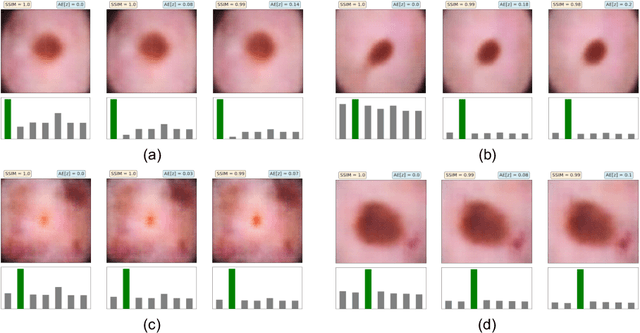
Abstract:The wide-spread adoption of representation learning technologies in clinical decision making strongly emphasizes the need for characterizing model reliability and enabling rigorous introspection of model behavior. While the former need is often addressed by incorporating uncertainty quantification strategies, the latter challenge is addressed using a broad class of interpretability techniques. In this paper, we argue that these two objectives are not necessarily disparate and propose to utilize prediction calibration to meet both objectives. More specifically, our approach is comprised of a calibration-driven learning method, which is also used to design an interpretability technique based on counterfactual reasoning. Furthermore, we introduce \textit{reliability plots}, a holistic evaluation mechanism for model reliability. Using a lesion classification problem with dermoscopy images, we demonstrate the effectiveness of our approach and infer interesting insights about the model behavior.
Calibrate and Prune: Improving Reliability of Lottery Tickets Through Prediction Calibration
Feb 11, 2020
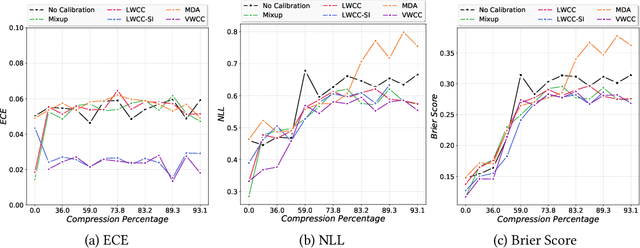
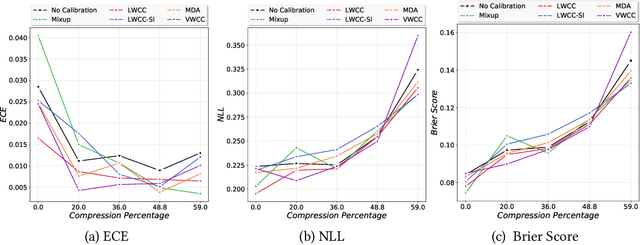
Abstract:The hypothesis that sub-network initializations (lottery) exist within the initializations of over-parameterized networks, which when trained in isolation produce highly generalizable models, has led to crucial insights into network initialization and has enabled computationally efficient inferencing. In order to realize the full potential of these pruning strategies, particularly when utilized in transfer learning scenarios, it is necessary to understand the behavior of winning tickets when they might overfit to the dataset characteristics. In supervised and semi-supervised learning, prediction calibration is a commonly adopted strategy to handle such inductive biases in models. In this paper, we study the impact of incorporating calibration strategies during model training on the quality of the resulting lottery tickets, using several evaluation metrics. More specifically, we incorporate a suite of calibration strategies to different combinations of architectures and datasets, and evaluate the fidelity of sub-networks retrained based on winning tickets. Furthermore, we report the generalization performance of tickets across distributional shifts, when the inductive biases are explicitly controlled using calibration mechanisms. Finally, we provide key insights and recommendations for obtaining reliable lottery tickets, which we demonstrate to achieve improved generalization.
Heteroscedastic Calibration of Uncertainty Estimators in Deep Learning
Oct 30, 2019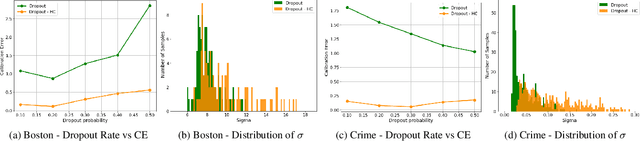
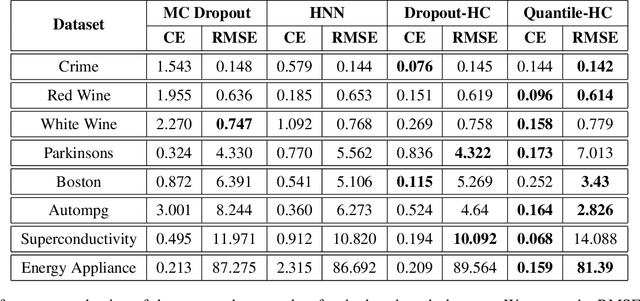
Abstract:The role of uncertainty quantification (UQ) in deep learning has become crucial with growing use of predictive models in high-risk applications. Though a large class of methods exists for measuring deep uncertainties, in practice, the resulting estimates are found to be poorly calibrated, thus making it challenging to translate them into actionable insights. A common workaround is to utilize a separate recalibration step, which adjusts the estimates to compensate for the miscalibration. Instead, we propose to repurpose the heteroscedastic regression objective as a surrogate for calibration and enable any existing uncertainty estimator to be inherently calibrated. In addition to eliminating the need for recalibration, this also regularizes the training process. Using regression experiments, we demonstrate the effectiveness of the proposed heteroscedastic calibration with two popular uncertainty estimators.
Learn-By-Calibrating: Using Calibration as a Training Objective
Oct 30, 2019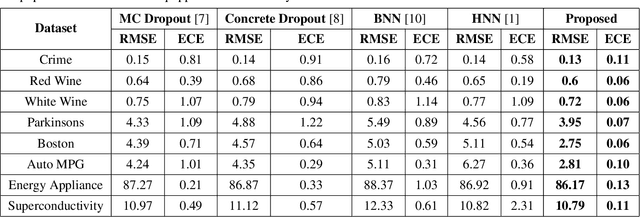
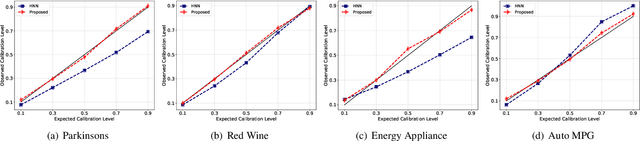
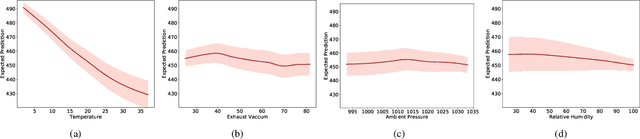
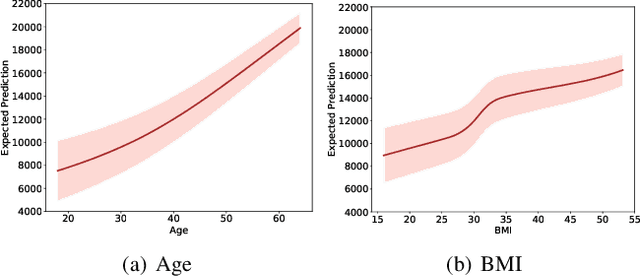
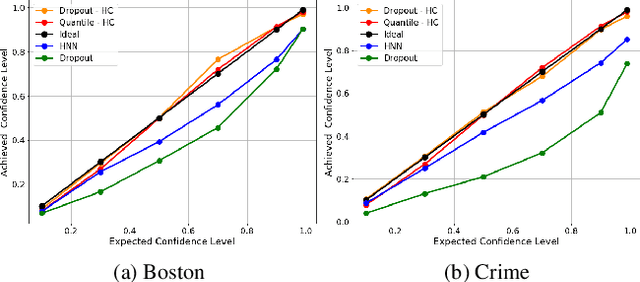
Abstract:Calibration error is commonly adopted for evaluating the quality of uncertainty estimators in deep neural networks. In this paper, we argue that such a metric is highly beneficial for training predictive models, even when we do not explicitly measure the uncertainties. This is conceptually similar to heteroscedastic neural networks that produce variance estimates for each prediction, with the key difference that we do not place a Gaussian prior on the predictions. We propose a novel algorithm that performs simultaneous interval estimation for different calibration levels and effectively leverages the intervals to refine the mean estimates. Our results show that, our approach is consistently superior to existing regularization strategies in deep regression models. Finally, we propose to augment partial dependence plots, a model-agnostic interpretability tool, with expected prediction intervals to reveal interesting dependencies between data and the target.
Building Calibrated Deep Models via Uncertainty Matching with Auxiliary Interval Predictors
Sep 09, 2019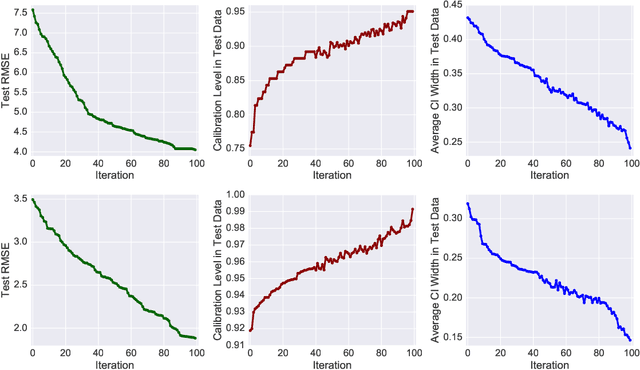
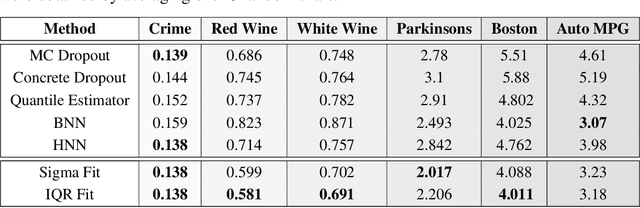
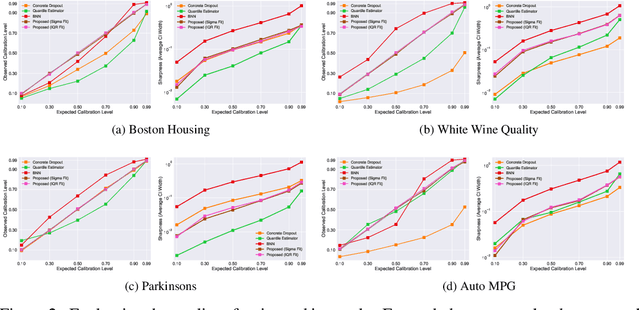
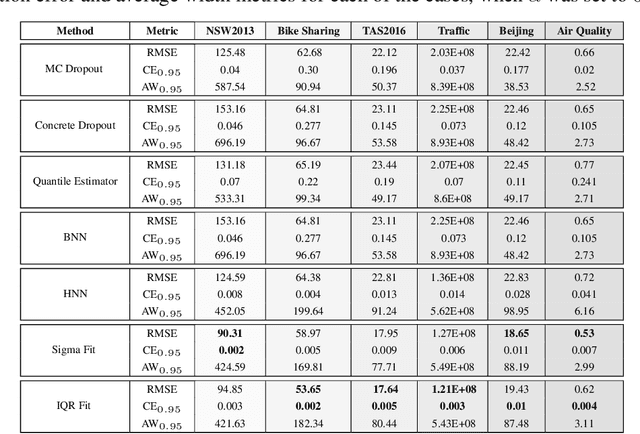
Abstract:With rapid adoption of deep learning in high-regret applications, the question of when and how much to trust these models often arises, which drives the need to quantify the inherent uncertainties. While identifying all sources that account for the stochasticity of learned models is challenging, it is common to augment predictions with confidence intervals to convey the expected variations in a model's behavior. In general, we require confidence intervals to be well-calibrated, reflect the true uncertainties, and to be sharp. However, most existing techniques for obtaining confidence intervals are known to produce unsatisfactory results in terms of at least one of those criteria. To address this challenge, we develop a novel approach for building calibrated estimators. More specifically, we construct separate models for predicting the target variable, and for estimating the confidence intervals, and pose a bi-level optimization problem that allows the predictive model to leverage estimates from the interval estimator through an \textit{uncertainty matching} strategy. Using experiments in regression, time-series forecasting, and object localization, we show that our approach achieves significant improvements over existing uncertainty quantification methods, both in terms of model fidelity and calibration error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge