Learn-By-Calibrating: Using Calibration as a Training Objective
Paper and Code
Oct 30, 2019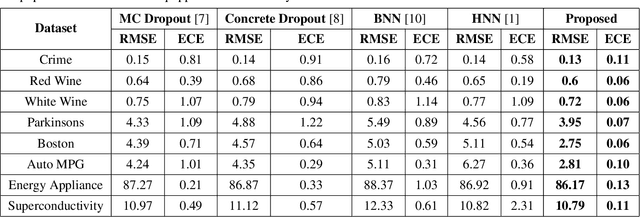
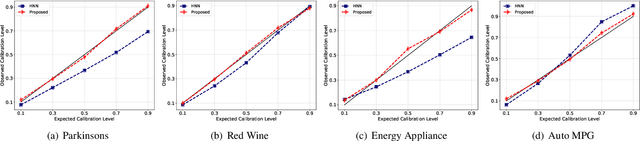
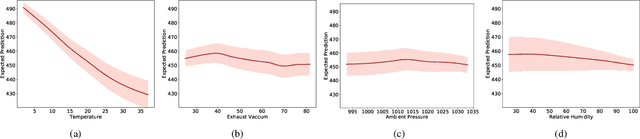
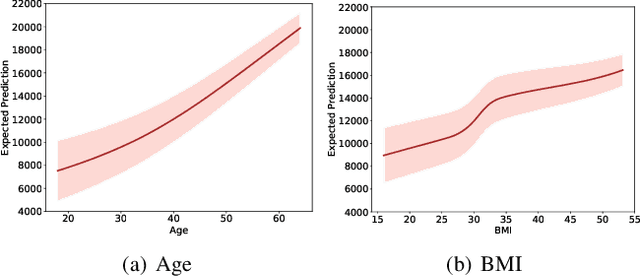
Calibration error is commonly adopted for evaluating the quality of uncertainty estimators in deep neural networks. In this paper, we argue that such a metric is highly beneficial for training predictive models, even when we do not explicitly measure the uncertainties. This is conceptually similar to heteroscedastic neural networks that produce variance estimates for each prediction, with the key difference that we do not place a Gaussian prior on the predictions. We propose a novel algorithm that performs simultaneous interval estimation for different calibration levels and effectively leverages the intervals to refine the mean estimates. Our results show that, our approach is consistently superior to existing regularization strategies in deep regression models. Finally, we propose to augment partial dependence plots, a model-agnostic interpretability tool, with expected prediction intervals to reveal interesting dependencies between data and the target.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge