Building Calibrated Deep Models via Uncertainty Matching with Auxiliary Interval Predictors

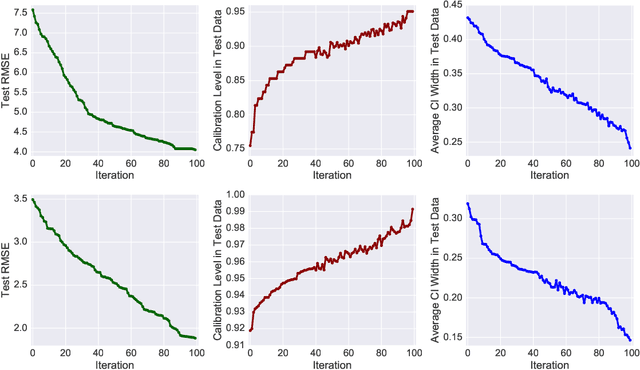
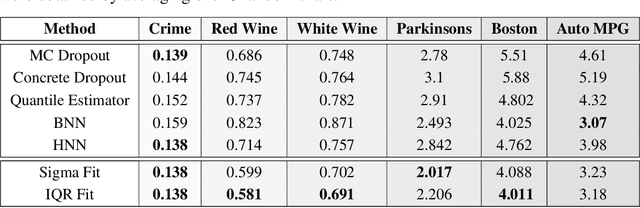
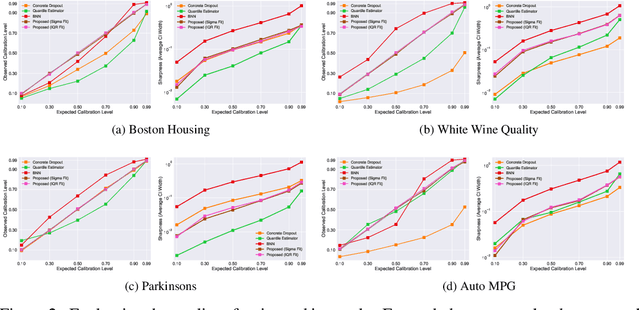
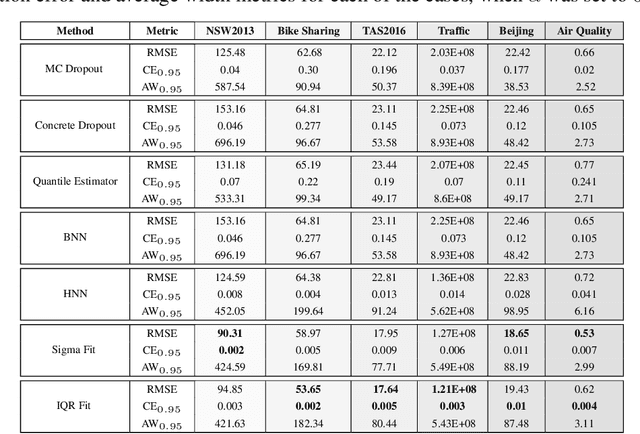
With rapid adoption of deep learning in high-regret applications, the question of when and how much to trust these models often arises, which drives the need to quantify the inherent uncertainties. While identifying all sources that account for the stochasticity of learned models is challenging, it is common to augment predictions with confidence intervals to convey the expected variations in a model's behavior. In general, we require confidence intervals to be well-calibrated, reflect the true uncertainties, and to be sharp. However, most existing techniques for obtaining confidence intervals are known to produce unsatisfactory results in terms of at least one of those criteria. To address this challenge, we develop a novel approach for building calibrated estimators. More specifically, we construct separate models for predicting the target variable, and for estimating the confidence intervals, and pose a bi-level optimization problem that allows the predictive model to leverage estimates from the interval estimator through an \textit{uncertainty matching} strategy. Using experiments in regression, time-series forecasting, and object localization, we show that our approach achieves significant improvements over existing uncertainty quantification methods, both in terms of model fidelity and calibration error.