Contextualized Machine Learning

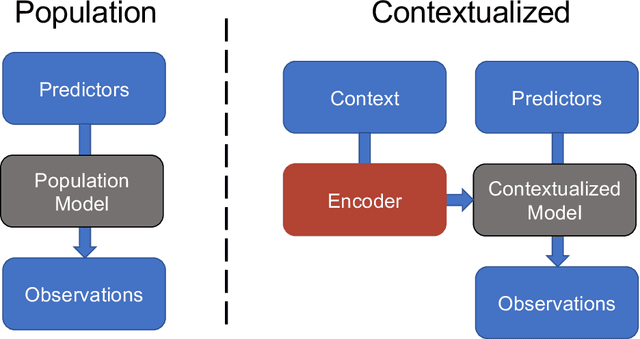
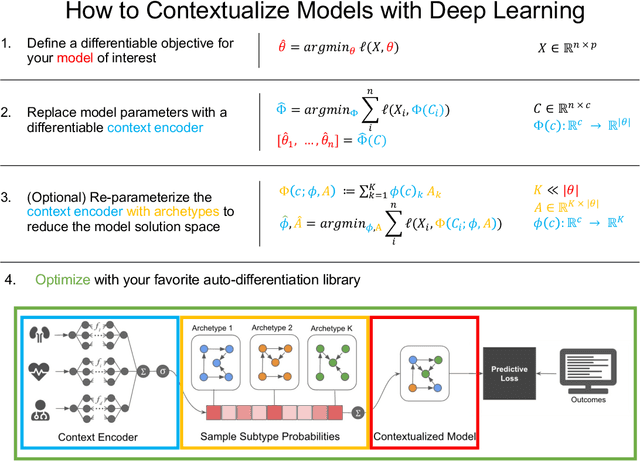
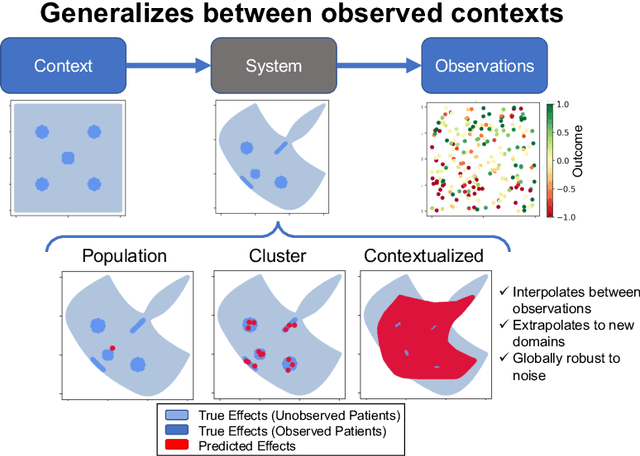
We examine Contextualized Machine Learning (ML), a paradigm for learning heterogeneous and context-dependent effects. Contextualized ML estimates heterogeneous functions by applying deep learning to the meta-relationship between contextual information and context-specific parametric models. This is a form of varying-coefficient modeling that unifies existing frameworks including cluster analysis and cohort modeling by introducing two reusable concepts: a context encoder which translates sample context into model parameters, and sample-specific model which operates on sample predictors. We review the process of developing contextualized models, nonparametric inference from contextualized models, and identifiability conditions of contextualized models. Finally, we present the open-source PyTorch package ContextualizedML.

Estimating Discontinuous Time-Varying Risk Factors and Treatment Benefits for COVID-19 with Interpretable ML

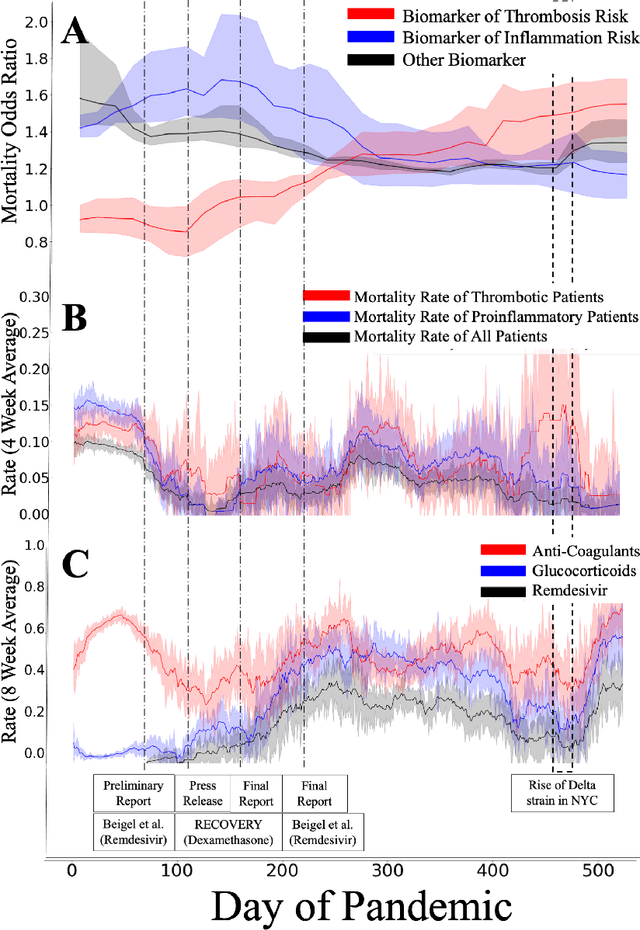
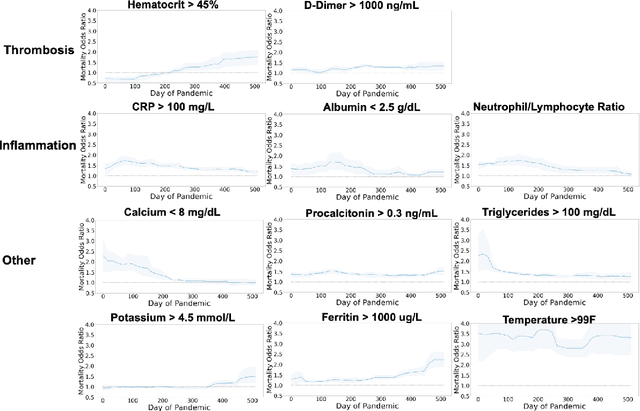
Treatment protocols, disease understanding, and viral characteristics changed over the course of the COVID-19 pandemic; as a result, the risks associated with patient comorbidities and biomarkers also changed. We add to the conversation regarding inflammation, hemostasis and vascular function in COVID-19 by performing a time-varying observational analysis of over 4000 patients hospitalized for COVID-19 in a New York City hospital system from March 2020 to August 2021. To perform this analysis, we apply tree-based generalized additive models with temporal interactions which recover discontinuous risk changes caused by discrete protocols changes. We find that the biomarkers of thrombosis increasingly predicted mortality from March 2020 to August 2021, while the association between biomarkers of inflammation and thrombosis weakened. Beyond COVID-19, this presents a straightforward methodology to estimate unknown and discontinuous time-varying effects.

On Dropout, Overfitting, and Interaction Effects in Deep Neural Networks

We examine Dropout through the perspective of interactions: learned effects that combine multiple input variables. Given $N$ variables, there are $O(N^2)$ possible pairwise interactions, $O(N^3)$ possible 3-way interactions, etc. We show that Dropout implicitly sets a learning rate for interaction effects that decays exponentially with the size of the interaction, corresponding to a regularizer that balances against the hypothesis space which grows exponentially with number of variables in the interaction. This understanding of Dropout has implications for the optimal Dropout rate: higher Dropout rates should be used when we need stronger regularization against spurious high-order interactions. This perspective also issues caution against using Dropout to measure term saliency because Dropout regularizes against terms for high-order interactions. Finally, this view of Dropout as a regularizer of interaction effects provides insight into the varying effectiveness of Dropout for different architectures and data sets. We also compare Dropout to regularization via weight decay and early stopping and find that it is difficult to obtain the same regularization effect for high-order interactions with these methods.

Purifying Interaction Effects with the Functional ANOVA: An Efficient Algorithm for Recovering Identifiable Additive Models

Recent methods for training generalized additive models (GAMs) with pairwise interactions achieve state-of-the-art accuracy on a variety of datasets. Adding interactions to GAMs, however, introduces an identifiability problem: effects can be freely moved between main effects and interaction effects without changing the model predictions. In some cases, this can lead to contradictory interpretations of the same underlying function. This is a critical problem because a central motivation of GAMs is model interpretability. In this paper, we use the Functional ANOVA decomposition to uniquely define interaction effects and thus produce identifiable additive models with purified interactions. To compute this decomposition, we present a fast, exact, mass-moving algorithm that transforms any piecewise-constant function (such as a tree-based model) into a purified, canonical representation. We apply this algorithm to several datasets and show large disparity, including contradictions, between the apparent and the purified effects.

Learning Sample-Specific Models with Low-Rank Personalized Regression

Modern applications of machine learning (ML) deal with increasingly heterogeneous datasets comprised of data collected from overlapping latent subpopulations. As a result, traditional models trained over large datasets may fail to recognize highly predictive localized effects in favour of weakly predictive global patterns. This is a problem because localized effects are critical to developing individualized policies and treatment plans in applications ranging from precision medicine to advertising. To address this challenge, we propose to estimate sample-specific models that tailor inference and prediction at the individual level. In contrast to classical ML models that estimate a single, complex model (or only a few complex models), our approach produces a model personalized to each sample. These sample-specific models can be studied to understand subgroup dynamics that go beyond coarse-grained class labels. Crucially, our approach does not assume that relationships between samples (e.g. a similarity network) are known a priori. Instead, we use unmodeled covariates to learn a latent distance metric over the samples. We apply this approach to financial, biomedical, and electoral data as well as simulated data and show that sample-specific models provide fine-grained interpretations of complicated phenomena without sacrificing predictive accuracy compared to state-of-the-art models such as deep neural networks.