SHAPCA: Consistent and Interpretable Explanations for Machine Learning Models on Spectroscopy Data

In recent years, machine learning models have been increasingly applied to spectroscopic datasets for chemical and biomedical analysis. For their successful adoption, particularly in clinical and safety-critical settings, professionals and researchers must be able to understand and trust the reasoning behind model predictions. However, the inherently high dimensionality and strong collinearity of spectroscopy data pose a fundamental challenge to model explainability. These properties not only complicate model training but also undermine the stability and consistency of explanations, leading to fluctuations in feature importance across repeated training runs. Feature extraction techniques have been used to reduce the input dimensionality; these new features hinder the connection between the prediction and the original signal. This study proposes SHAPCA, an explainable machine learning pipeline that combines Principal Component Analysis (for dimensionality reduction) and Shapely Additive exPlanations (for post hoc explanation) to provide explanations in the original input space, which a practitioner can interpret and link back to the biological components. The proposed framework enables analysis from both global and local perspectives, revealing the spectral bands that drive overall model behaviour as well as the instance-specific features that influence individual predictions. Numerical analysis demonstrated the interpretability of the results and greater consistency across different runs.

Agentic Design Patterns: A System-Theoretic Framework

With the development of foundation model (FM), agentic AI systems are getting more attention, yet their inherent issues like hallucination and poor reasoning, coupled with the frequent ad-hoc nature of system design, lead to unreliable and brittle applications. Existing efforts to characterise agentic design patterns often lack a rigorous systems-theoretic foundation, resulting in high-level or convenience-based taxonomies that are difficult to implement. This paper addresses this gap by introducing a principled methodology for engineering robust AI agents. We propose two primary contributions: first, a novel system-theoretic framework that deconstructs an agentic AI system into five core, interacting functional subsystems: Reasoning & World Model, Perception & Grounding, Action Execution, Learning & Adaptation, and Inter-Agent Communication. Second, derived from this architecture and directly mapped to a comprehensive taxonomy of agentic challenges, we present a collection of 12 agentic design patterns. These patterns - categorised as Foundational, Cognitive & Decisional, Execution & Interaction, and Adaptive & Learning - offer reusable, structural solutions to recurring problems in agent design. The utility of the framework is demonstrated by a case study on the ReAct framework, showing how the proposed patterns can rectify systemic architectural deficiencies. This work provides a foundational language and a structured methodology to standardise agentic design communication among researchers and engineers, leading to more modular, understandable, and reliable autonomous systems.

Questionnaire meets LLM: A Benchmark and Empirical Study of Structural Skills for Understanding Questions and Responses

Millions of people take surveys every day, from market polls and academic studies to medical questionnaires and customer feedback forms. These datasets capture valuable insights, but their scale and structure present a unique challenge for large language models (LLMs), which otherwise excel at few-shot reasoning over open-ended text. Yet, their ability to process questionnaire data or lists of questions crossed with hundreds of respondent rows remains underexplored. Current retrieval and survey analysis tools (e.g., Qualtrics, SPSS, REDCap) are typically designed for humans in the workflow, limiting such data integration with LLM and AI-empowered automation. This gap leaves scientists, surveyors, and everyday users without evidence-based guidance on how to best represent questionnaires for LLM consumption. We address this by introducing QASU (Questionnaire Analysis and Structural Understanding), a benchmark that probes six structural skills, including answer lookup, respondent count, and multi-hop inference, across six serialization formats and multiple prompt strategies. Experiments on contemporary LLMs show that choosing an effective format and prompt combination can improve accuracy by up to 8.8% points compared to suboptimal formats. For specific tasks, carefully adding a lightweight structural hint through self-augmented prompting can yield further improvements of 3-4% points on average. By systematically isolating format and prompting effects, our open source benchmark offers a simple yet versatile foundation for advancing both research and real-world practice in LLM-based questionnaire analysis.

Machine Learning Applications to Diffuse Reflectance Spectroscopy in Optical Diagnosis; A Systematic Review

Diffuse Reflectance Spectroscopy has demonstrated a strong aptitude for identifying and differentiating biological tissues. However, the broadband and smooth nature of these signals require algorithmic processing, as they are often difficult for the human eye to distinguish. The implementation of machine learning models for this task has demonstrated high levels of diagnostic accuracies and led to a wide range of proposed methodologies for applications in various illnesses and conditions. In this systematic review, we summarise the state of the art of these applications, highlight current gaps in research and identify future directions. This review was conducted in accordance with the PRISMA guidelines. 77 studies were retrieved and in-depth analysis was conducted. It is concluded that diffuse reflectance spectroscopy and machine learning have strong potential for tissue differentiation in clinical applications, but more rigorous sample stratification in tandem with in-vivo validation and explainable algorithm development is required going forward.

Multi-Agent Collaboration Mechanisms: A Survey of LLMs

With recent advances in Large Language Models (LLMs), Agentic AI has become phenomenal in real-world applications, moving toward multiple LLM-based agents to perceive, learn, reason, and act collaboratively. These LLM-based Multi-Agent Systems (MASs) enable groups of intelligent agents to coordinate and solve complex tasks collectively at scale, transitioning from isolated models to collaboration-centric approaches. This work provides an extensive survey of the collaborative aspect of MASs and introduces an extensible framework to guide future research. Our framework characterizes collaboration mechanisms based on key dimensions: actors (agents involved), types (e.g., cooperation, competition, or coopetition), structures (e.g., peer-to-peer, centralized, or distributed), strategies (e.g., role-based or model-based), and coordination protocols. Through a review of existing methodologies, our findings serve as a foundation for demystifying and advancing LLM-based MASs toward more intelligent and collaborative solutions for complex, real-world use cases. In addition, various applications of MASs across diverse domains, including 5G/6G networks, Industry 5.0, question answering, and social and cultural settings, are also investigated, demonstrating their wider adoption and broader impacts. Finally, we identify key lessons learned, open challenges, and potential research directions of MASs towards artificial collective intelligence.

Towards Fast Algorithms for the Preference Consistency Problem Based on Hierarchical Models

In this paper, we construct and compare algorithmic approaches to solve the Preference Consistency Problem for preference statements based on hierarchical models. Instances of this problem contain a set of preference statements that are direct comparisons (strict and non-strict) between some alternatives, and a set of evaluation functions by which all alternatives can be rated. An instance is consistent based on hierarchical preference models, if there exists an hierarchical model on the evaluation functions that induces an order relation on the alternatives by which all relations given by the preference statements are satisfied. Deciding if an instance is consistent is known to be NP-complete for hierarchical models. We develop three approaches to solve this decision problem. The first involves a Mixed Integer Linear Programming (MILP) formulation, the other two are recursive algorithms that are based on properties of the problem by which the search space can be pruned. Our experiments on synthetic data show that the recursive algorithms are faster than solving the MILP formulation and that the ratio between the running times increases extremely quickly.

Generation and Prediction of Difficult Model Counting Instances

We present a way to create small yet difficult model counting instances. Our generator is highly parameterizable: the number of variables of the instances it produces, as well as their number of clauses and the number of literals in each clause, can all be set to any value. Our instances have been tested on state of the art model counters, against other difficult model counting instances, in the Model Counting Competition. The smallest unsolved instances of the competition, both in terms of number of variables and number of clauses, were ours. We also observe a peak of difficulty when fixing the number of variables and varying the number of clauses, in both random instances and instances built by our generator. Using these results, we predict the parameter values for which the hardest to count instances will occur.

SATfeatPy - A Python-based Feature Extraction System for Satisfiability

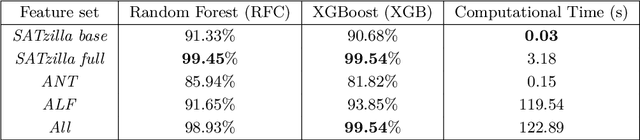
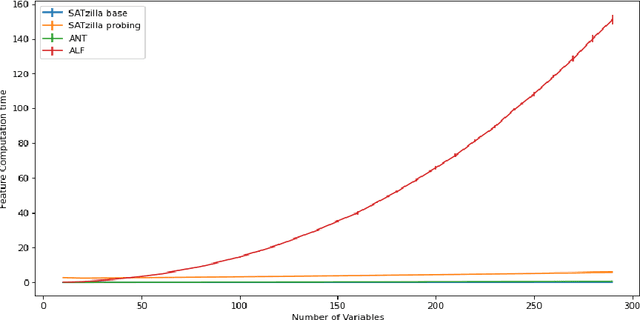
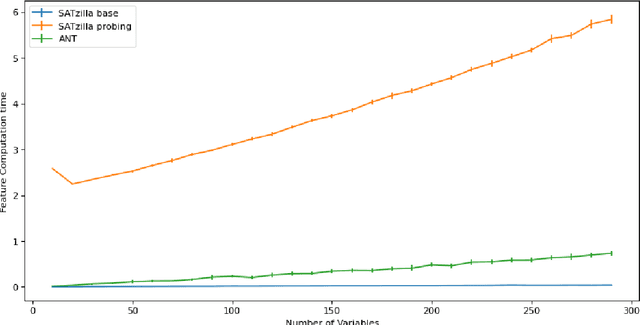
Feature extraction is a fundamental task in the application of machine learning methods to SAT solving. It is used in algorithm selection and configuration for solver portfolios and satisfiability classification. Many approaches have been proposed to extract meaningful attributes from CNF instances. Most of them lack a working/updated implementation, and the limited descriptions lack clarity affecting the reproducibility. Furthermore, the literature misses a comparison among the features. This paper introduces SATfeatPy, a library that offers feature extraction techniques for SAT problems in the CNF form. This package offers the implementation of all the structural and statistical features from there major papers in the field. The library is provided in an up-to-date, easy-to-use Python package alongside a detailed feature description. We show the high accuracy of SAT/UNSAT and problem category classification, using five sets of features generated using our library from a dataset of 3000 SAT and UNSAT instances, over ten different classes of problems. Finally, we compare the usefulness of the features and importance for predicting a SAT instance's original structure in an ablation study.

Finding Counterfactual Explanations through Constraint Relaxations

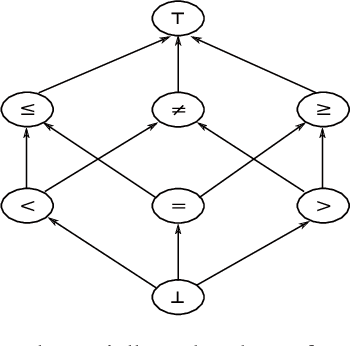
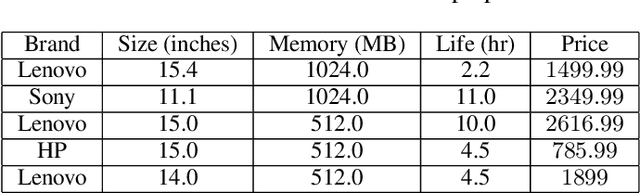
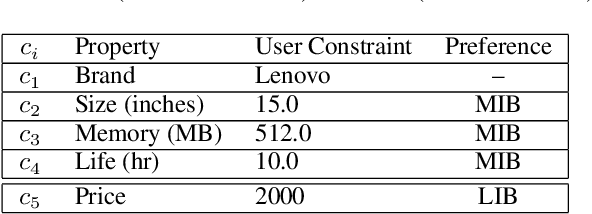
Interactive constraint systems often suffer from infeasibility (no solution) due to conflicting user constraints. A common approach to recover infeasibility is to eliminate the constraints that cause the conflicts in the system. This approach allows the system to provide an explanation as: "if the user is willing to drop out some of their constraints, there exists a solution". However, one can criticise this form of explanation as not being very informative. A counterfactual explanation is a type of explanation that can provide a basis for the user to recover feasibility by helping them understand which changes can be applied to their existing constraints rather than removing them. This approach has been extensively studied in the machine learning field, but requires a more thorough investigation in the context of constraint satisfaction. We propose an iterative method based on conflict detection and maximal relaxations in over-constrained constraint satisfaction problems to help compute a counterfactual explanation.

Solving Logic Grid Puzzles with an Algorithm that Imitates Human Behavior

We present in this paper our solver for logic grid puzzles. The approach used by our algorithm mimics the way a human would try to solve the same problem. Every progress made during the solving process is accompanied by a detailed explanation of our program's reasoning. Since this reasoning is based on the same heuristics that a human would employ, the user can easily follow the given explanation.