Gilles Simonin
Finding Robust Solutions to Stable Marriage
Oct 27, 2017
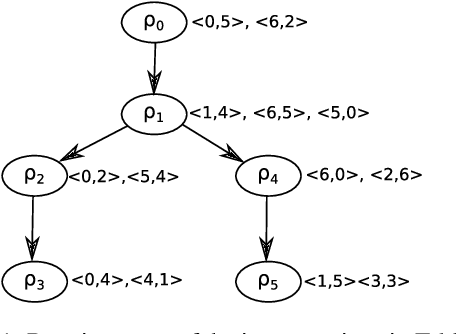
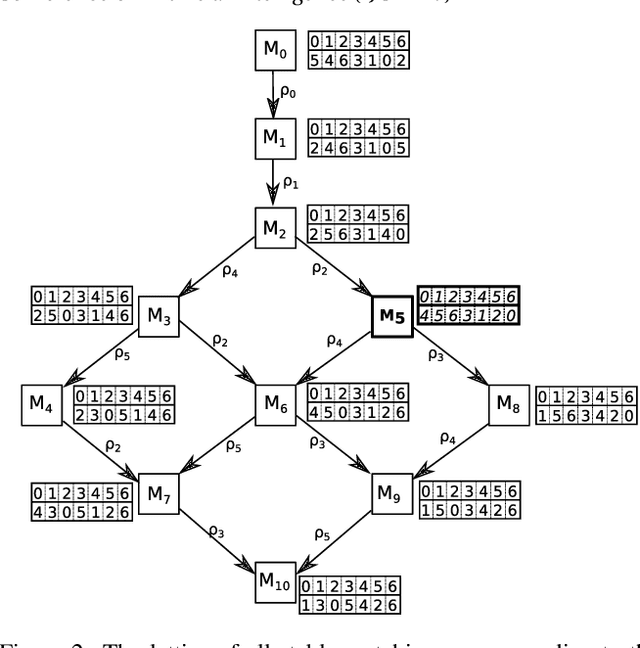
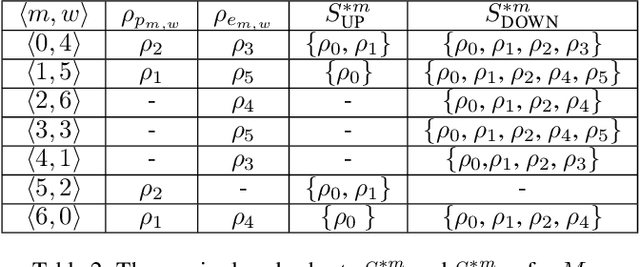
Abstract:We study the notion of robustness in stable matching problems. We first define robustness by introducing (a,b)-supermatches. An $(a,b)$-supermatch is a stable matching in which if $a$ pairs break up it is possible to find another stable matching by changing the partners of those $a$ pairs and at most $b$ other pairs. In this context, we define the most robust stable matching as a $(1,b)$-supermatch where b is minimum. We show that checking whether a given stable matching is a $(1,b)$-supermatch can be done in polynomial time. Next, we use this procedure to design a constraint programming model, a local search approach, and a genetic algorithm to find the most robust stable matching. Our empirical evaluation on large instances show that local search outperforms the other approaches.
On the Complexity of Robust Stable Marriage
Oct 27, 2017
Abstract:Robust Stable Marriage (RSM) is a variant of the classical Stable Marriage problem, where the robustness of a given stable matching is measured by the number of modifications required for repairing it in case an unforeseen event occurs. We focus on the complexity of finding an (a,b)-supermatch. An (a,b)-supermatch is defined as a stable matching in which if any 'a' (non-fixed) men/women break up it is possible to find another stable matching by changing the partners of those 'a' men/women and also the partners of at most 'b' other couples. In order to show deciding if there exists an (a,b)-supermatch is NP-Complete, we first introduce a SAT formulation that is NP-Complete by using Schaefer's Dichotomy Theorem. Then, we show the equivalence between the SAT formulation and finding a (1,1)-supermatch on a specific family of instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge