Finding Robust Solutions to Stable Marriage
Paper and Code
Oct 27, 2017
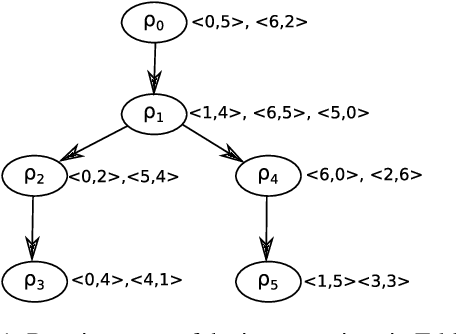
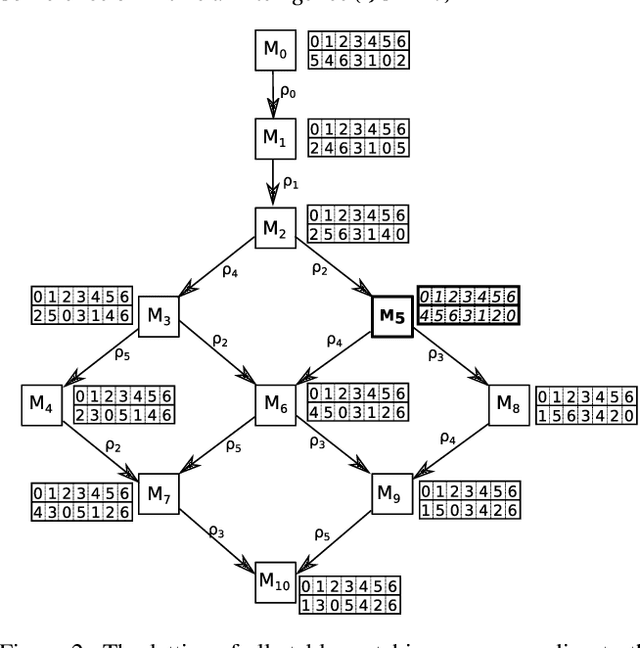
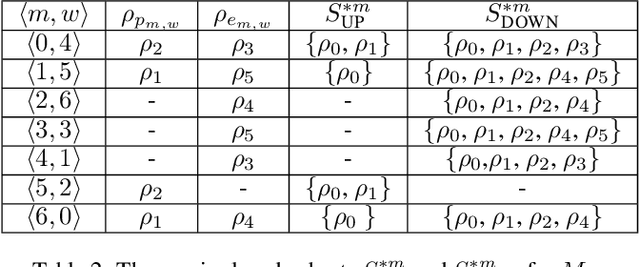
We study the notion of robustness in stable matching problems. We first define robustness by introducing (a,b)-supermatches. An $(a,b)$-supermatch is a stable matching in which if $a$ pairs break up it is possible to find another stable matching by changing the partners of those $a$ pairs and at most $b$ other pairs. In this context, we define the most robust stable matching as a $(1,b)$-supermatch where b is minimum. We show that checking whether a given stable matching is a $(1,b)$-supermatch can be done in polynomial time. Next, we use this procedure to design a constraint programming model, a local search approach, and a genetic algorithm to find the most robust stable matching. Our empirical evaluation on large instances show that local search outperforms the other approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge