Finding Counterfactual Explanations through Constraint Relaxations

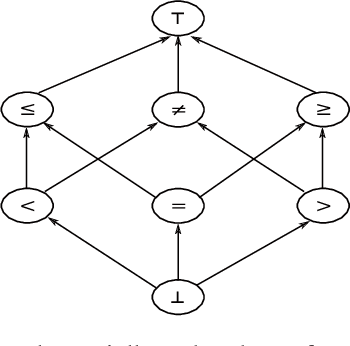
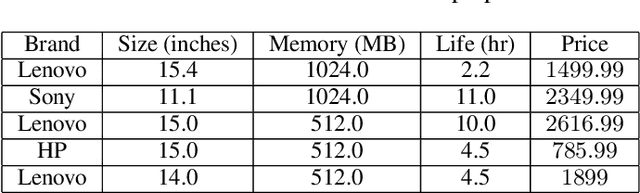
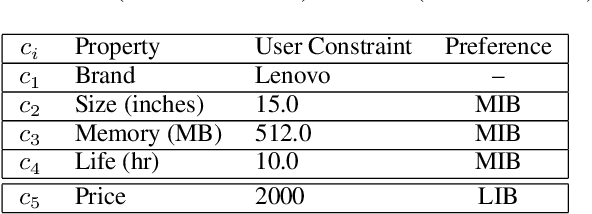
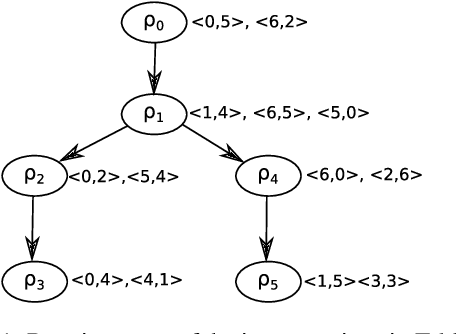
Interactive constraint systems often suffer from infeasibility (no solution) due to conflicting user constraints. A common approach to recover infeasibility is to eliminate the constraints that cause the conflicts in the system. This approach allows the system to provide an explanation as: "if the user is willing to drop out some of their constraints, there exists a solution". However, one can criticise this form of explanation as not being very informative. A counterfactual explanation is a type of explanation that can provide a basis for the user to recover feasibility by helping them understand which changes can be applied to their existing constraints rather than removing them. This approach has been extensively studied in the machine learning field, but requires a more thorough investigation in the context of constraint satisfaction. We propose an iterative method based on conflict detection and maximal relaxations in over-constrained constraint satisfaction problems to help compute a counterfactual explanation.

Finding Robust Solutions to Stable Marriage

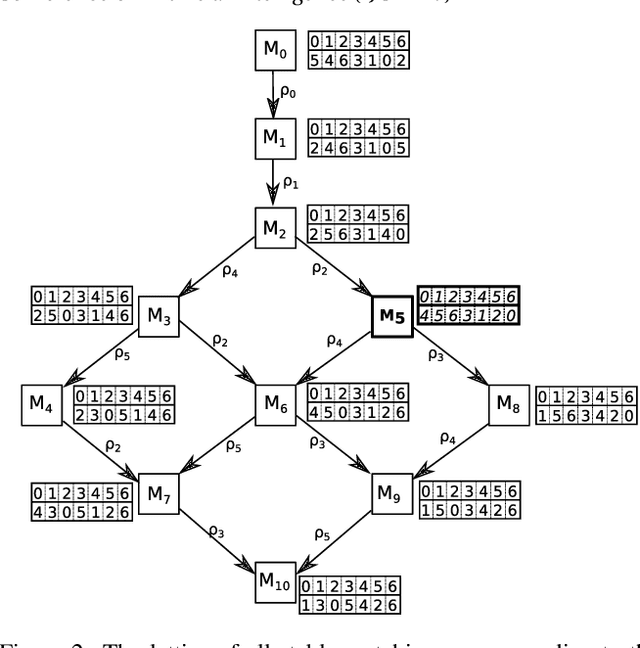
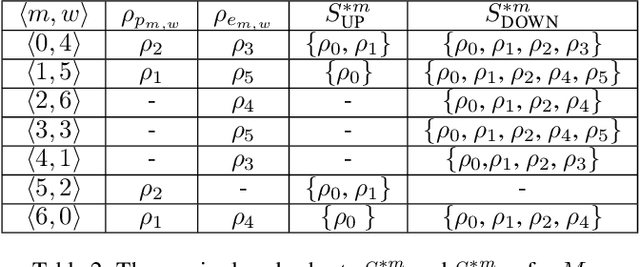
We study the notion of robustness in stable matching problems. We first define robustness by introducing (a,b)-supermatches. An $(a,b)$-supermatch is a stable matching in which if $a$ pairs break up it is possible to find another stable matching by changing the partners of those $a$ pairs and at most $b$ other pairs. In this context, we define the most robust stable matching as a $(1,b)$-supermatch where b is minimum. We show that checking whether a given stable matching is a $(1,b)$-supermatch can be done in polynomial time. Next, we use this procedure to design a constraint programming model, a local search approach, and a genetic algorithm to find the most robust stable matching. Our empirical evaluation on large instances show that local search outperforms the other approaches.

On the Complexity of Robust Stable Marriage

Robust Stable Marriage (RSM) is a variant of the classical Stable Marriage problem, where the robustness of a given stable matching is measured by the number of modifications required for repairing it in case an unforeseen event occurs. We focus on the complexity of finding an (a,b)-supermatch. An (a,b)-supermatch is defined as a stable matching in which if any 'a' (non-fixed) men/women break up it is possible to find another stable matching by changing the partners of those 'a' men/women and also the partners of at most 'b' other couples. In order to show deciding if there exists an (a,b)-supermatch is NP-Complete, we first introduce a SAT formulation that is NP-Complete by using Schaefer's Dichotomy Theorem. Then, we show the equivalence between the SAT formulation and finding a (1,1)-supermatch on a specific family of instances.