Facilitating Knowledge Sharing from Domain Experts to Data Scientists for Building NLP Models

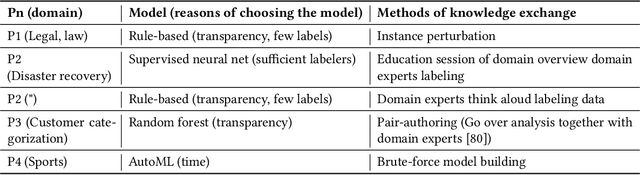
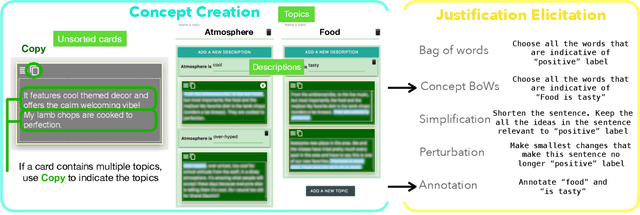
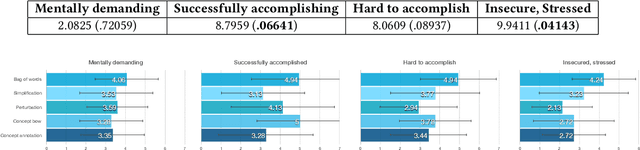
Data scientists face a steep learning curve in understanding a new domain for which they want to build machine learning (ML) models. While input from domain experts could offer valuable help, such input is often limited, expensive, and generally not in a form readily consumable by a model development pipeline. In this paper, we propose Ziva, a framework to guide domain experts in sharing essential domain knowledge to data scientists for building NLP models. With Ziva, experts are able to distill and share their domain knowledge using domain concept extractors and five types of label justification over a representative data sample. The design of Ziva is informed by preliminary interviews with data scientists, in order to understand current practices of domain knowledge acquisition process for ML development projects. To assess our design, we run a mix-method case-study to evaluate how Ziva can facilitate interaction of domain experts and data scientists. Our results highlight that (1) domain experts are able to use Ziva to provide rich domain knowledge, while maintaining low mental load and stress levels; and (2) data scientists find Ziva's output helpful for learning essential information about the domain, offering scalability of information, and lowering the burden on domain experts to share knowledge. We conclude this work by experimenting with building NLP models using the Ziva output by our case study.

A Survey of the State of Explainable AI for Natural Language Processing

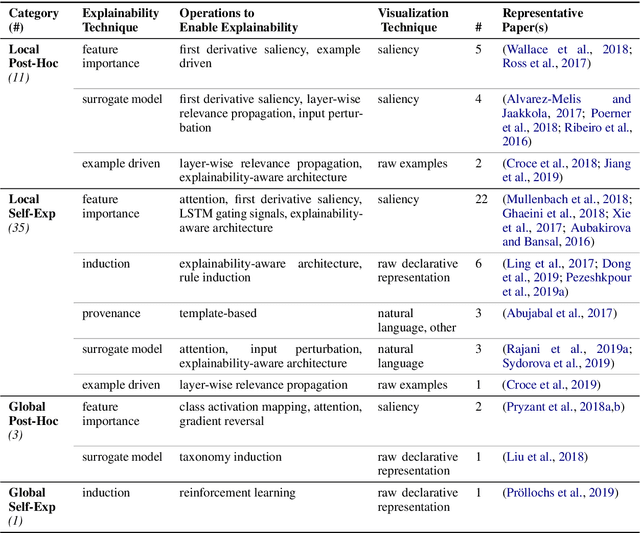
Recent years have seen important advances in the quality of state-of-the-art models, but this has come at the expense of models becoming less interpretable. This survey presents an overview of the current state of Explainable AI (XAI), considered within the domain of Natural Language Processing (NLP). We discuss the main categorization of explanations, as well as the various ways explanations can be arrived at and visualized. We detail the operations and explainability techniques currently available for generating explanations for NLP model predictions, to serve as a resource for model developers in the community. Finally, we point out the current gaps and encourage directions for future work in this important research area.

Robust Partially-Compressed Least-Squares

Randomized matrix compression techniques, such as the Johnson-Lindenstrauss transform, have emerged as an effective and practical way for solving large-scale problems efficiently. With a focus on computational efficiency, however, forsaking solutions quality and accuracy becomes the trade-off. In this paper, we investigate compressed least-squares problems and propose new models and algorithms that address the issue of error and noise introduced by compression. While maintaining computational efficiency, our models provide robust solutions that are more accurate--relative to solutions of uncompressed least-squares--than those of classical compressed variants. We introduce tools from robust optimization together with a form of partial compression to improve the error-time trade-offs of compressed least-squares solvers. We develop an efficient solution algorithm for our Robust Partially-Compressed (RPC) model based on a reduction to a one-dimensional search. We also derive the first approximation error bounds for Partially-Compressed least-squares solutions. Empirical results comparing numerous alternatives suggest that robust and partially compressed solutions are effectively insulated against aggressive randomized transforms.