Image Generation Via Minimizing Fréchet Distance in Discriminator Feature Space

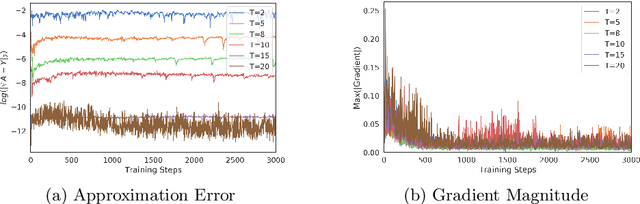
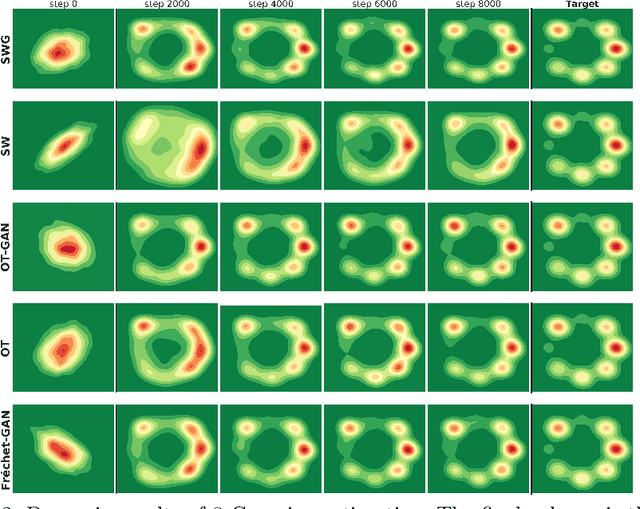
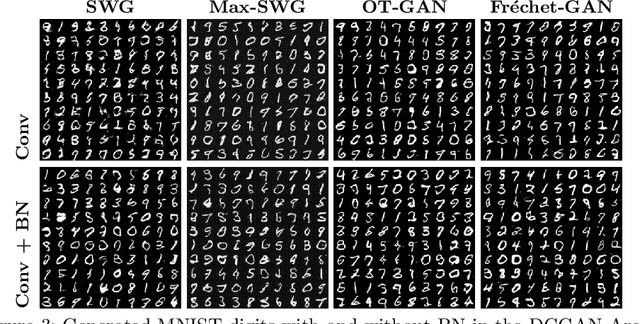
For a given image generation problem, the intrinsic image manifold is often low dimensional. We use the intuition that it is much better to train the GAN generator by minimizing the distributional distance between real and generated images in a small dimensional feature space representing such a manifold than on the original pixel-space. We use the feature space of the GAN discriminator for such a representation. For distributional distance, we employ one of two choices: the Fr\'{e}chet distance or direct optimal transport (OT); these respectively lead us to two new GAN methods: Fr\'{e}chet-GAN and OT-GAN. The idea of employing Fr\'{e}chet distance comes from the success of Fr\'{e}chet Inception Distance as a solid evaluation metric in image generation. Fr\'{e}chet-GAN is attractive in several ways. We propose an efficient, numerically stable approach to calculate the Fr\'{e}chet distance and its gradient. The Fr\'{e}chet distance estimation requires a significantly less computation time than OT; this allows Fr\'{e}chet-GAN to use much larger mini-batch size in training than OT. More importantly, we conduct experiments on a number of benchmark datasets and show that Fr\'{e}chet-GAN (in particular) and OT-GAN have significantly better image generation capabilities than the existing representative primal and dual GAN approaches based on the Wasserstein distance.

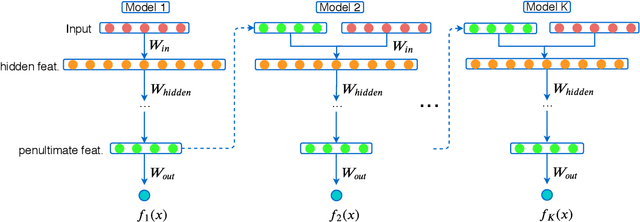
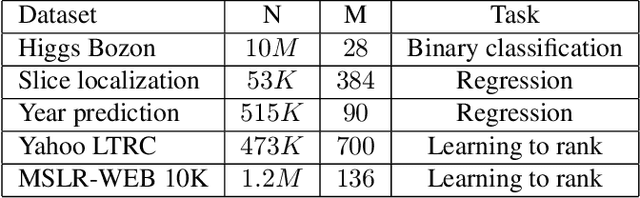
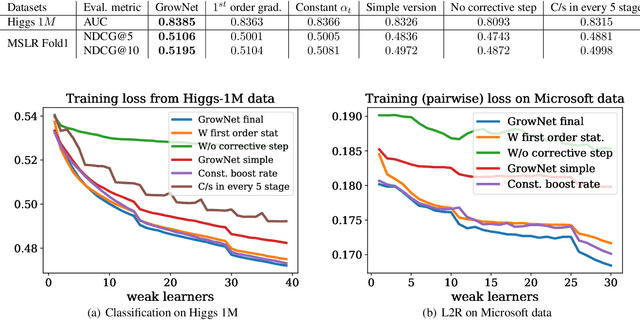
Gradient Boosting Neural Networks: GrowNet

A novel gradient boosting framework is proposed where shallow neural networks are employed as "weak learners". General loss functions are considered under this unified framework with specific examples presented for classification, regression and learning to rank. A fully corrective step is incorporated to remedy the pitfall of greedy function approximation of classic gradient boosting decision tree. The proposed model rendered state-of-the-art results in all three tasks on multiple datasets. An ablation study is performed to shed light on the effect of each model components and model hyperparameters.

Geometry Aware Mappings for High Dimensional Sparse Factors

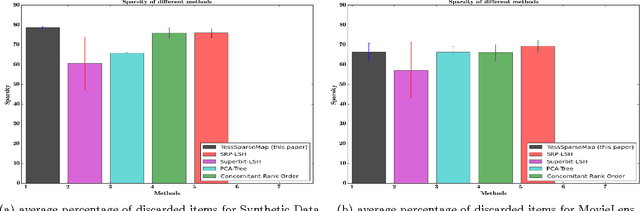
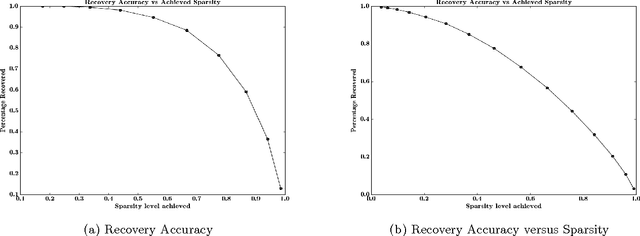
While matrix factorisation models are ubiquitous in large scale recommendation and search, real time application of such models requires inner product computations over an intractably large set of item factors. In this manuscript we present a novel framework that uses the inverted index representation to exploit structural properties of sparse vectors to significantly reduce the run time computational cost of factorisation models. We develop techniques that use geometry aware permutation maps on a tessellated unit sphere to obtain high dimensional sparse embeddings for latent factors with sparsity patterns related to angular closeness of the original latent factors. We also design several efficient and deterministic realisations within this framework and demonstrate with experiments that our techniques lead to faster run time operation with minimal loss of accuracy.

Generalized Linear Models for Aggregated Data

Databases in domains such as healthcare are routinely released to the public in aggregated form. Unfortunately, naive modeling with aggregated data may significantly diminish the accuracy of inferences at the individual level. This paper addresses the scenario where features are provided at the individual level, but the target variables are only available as histogram aggregates or order statistics. We consider a limiting case of generalized linear modeling when the target variables are only known up to permutation, and explore how this relates to permutation testing; a standard technique for assessing statistical dependency. Based on this relationship, we propose a simple algorithm to estimate the model parameters and individual level inferences via alternating imputation and standard generalized linear model fitting. Our results suggest the effectiveness of the proposed approach when, in the original data, permutation testing accurately ascertains the veracity of the linear relationship. The framework is extended to general histogram data with larger bins - with order statistics such as the median as a limiting case. Our experimental results on simulated data and aggregated healthcare data suggest a diminishing returns property with respect to the granularity of the histogram - when a linear relationship holds in the original data, the targets can be predicted accurately given relatively coarse histograms.

Monotone Retargeting for Unsupervised Rank Aggregation with Object Features

Learning the true ordering between objects by aggregating a set of expert opinion rank order lists is an important and ubiquitous problem in many applications ranging from social choice theory to natural language processing and search aggregation. We study the problem of unsupervised rank aggregation where no ground truth ordering information in available, neither about the true preference ordering between any set of objects nor about the quality of individual rank lists. Aggregating the often inconsistent and poor quality rank lists in such an unsupervised manner is a highly challenging problem, and standard consensus-based methods are often ill-defined, and difficult to solve. In this manuscript we propose a novel framework to bypass these issues by using object attributes to augment the standard rank aggregation framework. We design algorithms that learn joint models on both rank lists and object features to obtain an aggregated rank ordering that is more accurate and robust, and also helps weed out rank lists of dubious validity. We validate our techniques on synthetic datasets where our algorithm is able to estimate the true rank ordering even when the rank lists are corrupted. Experiments on three real datasets, MQ2008, MQ2008 and OHSUMED, show that using object features can result in significant improvement in performance over existing rank aggregation methods that do not use object information. Furthermore, when at least some of the rank lists are of high quality, our methods are able to effectively exploit their high expertise to output an aggregated rank ordering of great accuracy.