Geometry Aware Mappings for High Dimensional Sparse Factors
Paper and Code
May 16, 2016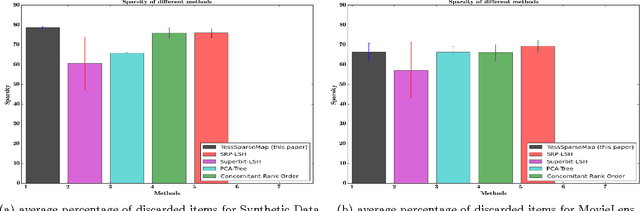
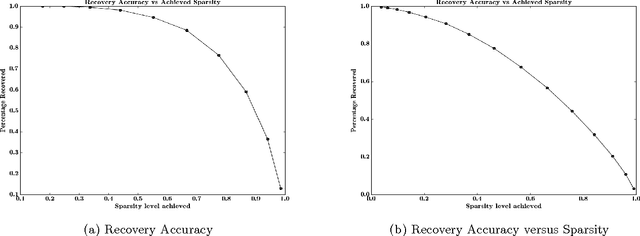
While matrix factorisation models are ubiquitous in large scale recommendation and search, real time application of such models requires inner product computations over an intractably large set of item factors. In this manuscript we present a novel framework that uses the inverted index representation to exploit structural properties of sparse vectors to significantly reduce the run time computational cost of factorisation models. We develop techniques that use geometry aware permutation maps on a tessellated unit sphere to obtain high dimensional sparse embeddings for latent factors with sparsity patterns related to angular closeness of the original latent factors. We also design several efficient and deterministic realisations within this framework and demonstrate with experiments that our techniques lead to faster run time operation with minimal loss of accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge