Geometry Aware Mappings for High Dimensional Sparse Factors

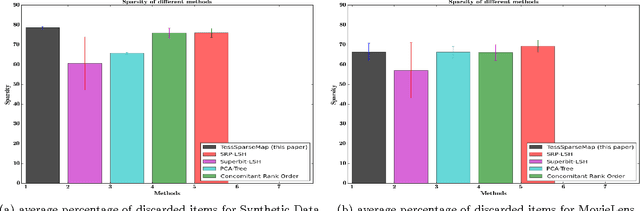
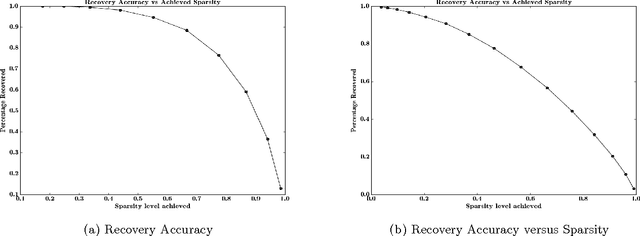
While matrix factorisation models are ubiquitous in large scale recommendation and search, real time application of such models requires inner product computations over an intractably large set of item factors. In this manuscript we present a novel framework that uses the inverted index representation to exploit structural properties of sparse vectors to significantly reduce the run time computational cost of factorisation models. We develop techniques that use geometry aware permutation maps on a tessellated unit sphere to obtain high dimensional sparse embeddings for latent factors with sparsity patterns related to angular closeness of the original latent factors. We also design several efficient and deterministic realisations within this framework and demonstrate with experiments that our techniques lead to faster run time operation with minimal loss of accuracy.

Large-Scale Distributed Bayesian Matrix Factorization using Stochastic Gradient MCMC

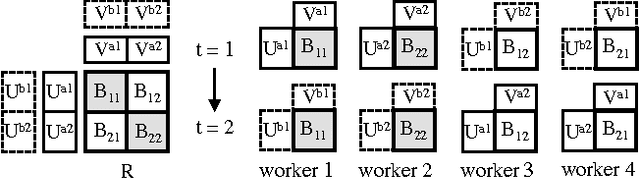
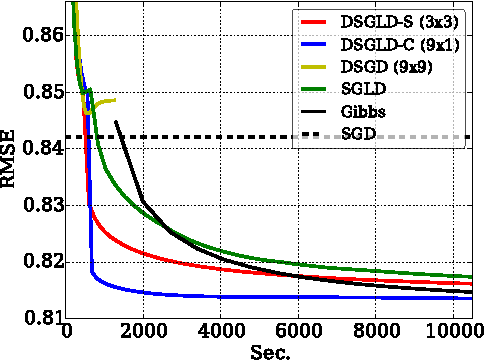
Despite having various attractive qualities such as high prediction accuracy and the ability to quantify uncertainty and avoid over-fitting, Bayesian Matrix Factorization has not been widely adopted because of the prohibitive cost of inference. In this paper, we propose a scalable distributed Bayesian matrix factorization algorithm using stochastic gradient MCMC. Our algorithm, based on Distributed Stochastic Gradient Langevin Dynamics, can not only match the prediction accuracy of standard MCMC methods like Gibbs sampling, but at the same time is as fast and simple as stochastic gradient descent. In our experiments, we show that our algorithm can achieve the same level of prediction accuracy as Gibbs sampling an order of magnitude faster. We also show that our method reduces the prediction error as fast as distributed stochastic gradient descent, achieving a 4.1% improvement in RMSE for the Netflix dataset and an 1.8% for the Yahoo music dataset.