On Symbolically Encoding the Behavior of Random Forests

Recent work has shown that the input-output behavior of some machine learning systems can be captured symbolically using Boolean expressions or tractable Boolean circuits, which facilitates reasoning about the behavior of these systems. While most of the focus has been on systems with Boolean inputs and outputs, we address systems with discrete inputs and outputs, including ones with discretized continuous variables as in systems based on decision trees. We also focus on the suitability of encodings for computing prime implicants, which have recently played a central role in explaining the decisions of machine learning systems. We show some key distinctions with encodings for satisfiability, and propose an encoding that is sound and complete for the given task.

A New Perspective on Learning Context-Specific Independence

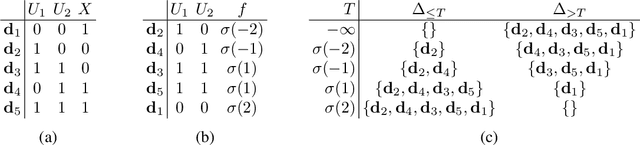
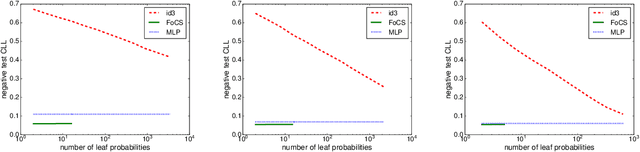
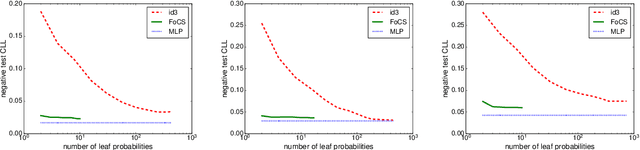
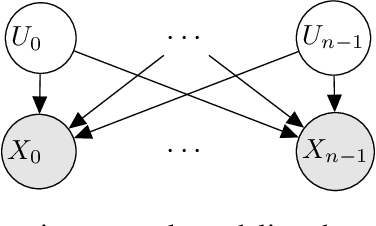
Local structure such as context-specific independence (CSI) has received much attention in the probabilistic graphical model (PGM) literature, as it facilitates the modeling of large complex systems, as well as for reasoning with them. In this paper, we provide a new perspective on how to learn CSIs from data. We propose to first learn a functional and parameterized representation of a conditional probability table (CPT), such as a neural network. Next, we quantize this continuous function, into an arithmetic circuit representation that facilitates efficient inference. In the first step, we can leverage the many powerful tools that have been developed in the machine learning literature. In the second step, we exploit more recently-developed analytic tools from explainable AI, for the purposes of learning CSIs. Finally, we contrast our approach, empirically and conceptually, with more traditional variable-splitting approaches, that search for CSIs more explicitly.

On Tractable Representations of Binary Neural Networks

We consider the compilation of a binary neural network's decision function into tractable representations such as Ordered Binary Decision Diagrams (OBDDs) and Sentential Decision Diagrams (SDDs). Obtaining this function as an OBDD/SDD facilitates the explanation and formal verification of a neural network's behavior. First, we consider the task of verifying the robustness of a neural network, and show how we can compute the expected robustness of a neural network, given an OBDD/SDD representation of it. Next, we consider a more efficient approach for compiling neural networks, based on a pseudo-polynomial time algorithm for compiling a neuron. We then provide a case study in a handwritten digits dataset, highlighting how two neural networks trained from the same dataset can have very high accuracies, yet have very different levels of robustness. Finally, in experiments, we show that it is feasible to obtain compact representations of neural networks as SDDs.

On the Relative Expressiveness of Bayesian and Neural Networks

A neural network computes a function. A central property of neural networks is that they are "universal approximators:" for a given continuous function, there exists a neural network that can approximate it arbitrarily well, given enough neurons (and some additional assumptions). In contrast, a Bayesian network is a model, but each of its queries can be viewed as computing a function. In this paper, we identify some key distinctions between the functions computed by neural networks and those by marginal Bayesian network queries, showing that the former are more expressive than the latter. Moreover, we propose a simple augmentation to Bayesian networks (a testing operator), which enables their marginal queries to become "universal approximators."

A Symbolic Approach to Explaining Bayesian Network Classifiers

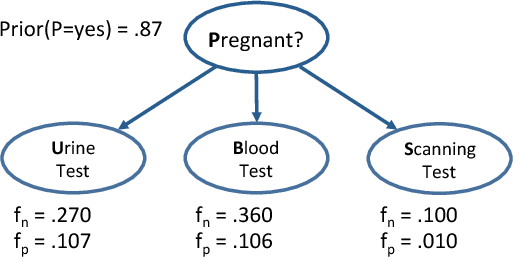
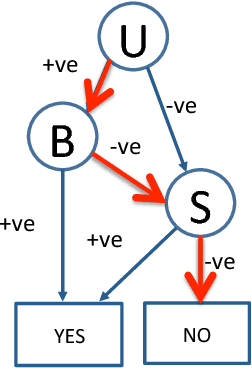
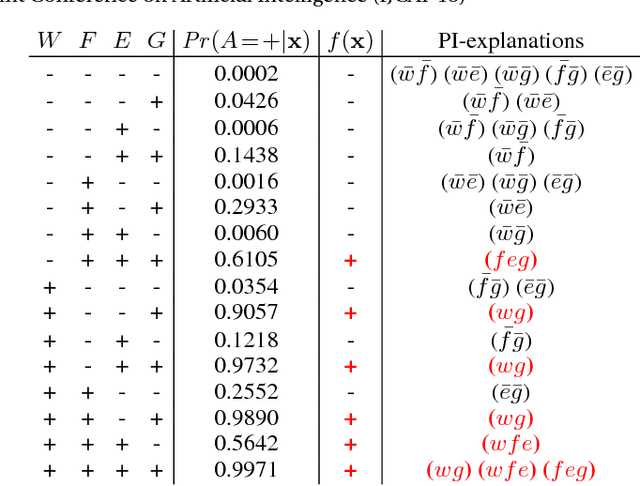
We propose an approach for explaining Bayesian network classifiers, which is based on compiling such classifiers into decision functions that have a tractable and symbolic form. We introduce two types of explanations for why a classifier may have classified an instance positively or negatively and suggest algorithms for computing these explanations. The first type of explanation identifies a minimal set of the currently active features that is responsible for the current classification, while the second type of explanation identifies a minimal set of features whose current state (active or not) is sufficient for the classification. We consider in particular the compilation of Naive and Latent-Tree Bayesian network classifiers into Ordered Decision Diagrams (ODDs), providing a context for evaluating our proposal using case studies and experiments based on classifiers from the literature.

On Relaxing Determinism in Arithmetic Circuits

The past decade has seen a significant interest in learning tractable probabilistic representations. Arithmetic circuits (ACs) were among the first proposed tractable representations, with some subsequent representations being instances of ACs with weaker or stronger properties. In this paper, we provide a formal basis under which variants on ACs can be compared, and where the precise roles and semantics of their various properties can be made more transparent. This allows us to place some recent developments on ACs in a clearer perspective and to also derive new results for ACs. This includes an exponential separation between ACs with and without determinism; completeness and incompleteness results; and tractability results (or lack thereof) when computing most probable explanations (MPEs).

Dual Decomposition from the Perspective of Relax, Compensate and then Recover

Relax, Compensate and then Recover (RCR) is a paradigm for approximate inference in probabilistic graphical models that has previously provided theoretical and practical insights on iterative belief propagation and some of its generalizations. In this paper, we characterize the technique of dual decomposition in the terms of RCR, viewing it as a specific way to compensate for relaxed equivalence constraints. Among other insights gathered from this perspective, we propose novel heuristics for recovering relaxed equivalence constraints with the goal of incrementally tightening dual decomposition approximations, all the way to reaching exact solutions. We also show empirically that recovering equivalence constraints can sometimes tighten the corresponding approximation (and obtaining exact results), without increasing much the complexity of inference.

Efficient Algorithms for Bayesian Network Parameter Learning from Incomplete Data

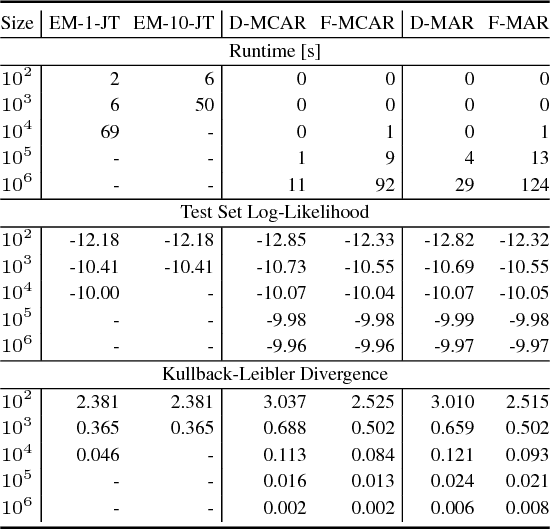
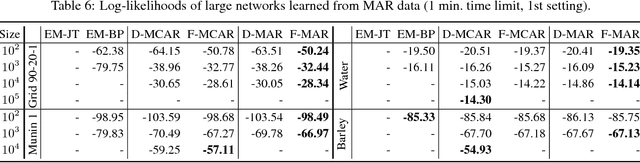
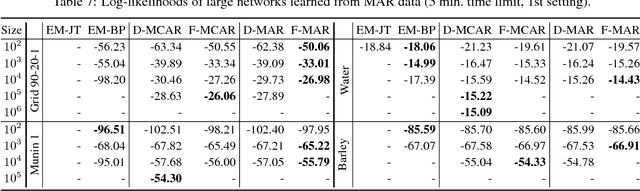
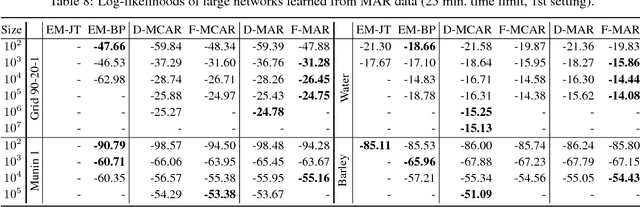
We propose an efficient family of algorithms to learn the parameters of a Bayesian network from incomplete data. In contrast to textbook approaches such as EM and the gradient method, our approach is non-iterative, yields closed form parameter estimates, and eliminates the need for inference in a Bayesian network. Our approach provides consistent parameter estimates for missing data problems that are MCAR, MAR, and in some cases, MNAR. Empirically, our approach is orders of magnitude faster than EM (as our approach requires no inference). Given sufficient data, we learn parameters that can be orders of magnitude more accurate.

New Advances and Theoretical Insights into EDML

EDML is a recently proposed algorithm for learning MAP parameters in Bayesian networks. In this paper, we present a number of new advances and insights on the EDML algorithm. First, we provide the multivalued extension of EDML, originally proposed for Bayesian networks over binary variables. Next, we identify a simplified characterization of EDML that further implies a simple fixed-point algorithm for the convex optimization problem that underlies it. This characterization further reveals a connection between EDML and EM: a fixed point of EDML is a fixed point of EM, and vice versa. We thus identify also a new characterization of EM fixed points, but in the semantics of EDML. Finally, we propose a hybrid EDML/EM algorithm that takes advantage of the improved empirical convergence behavior of EDML, while maintaining the monotonic improvement property of EM.

Lifted Relax, Compensate and then Recover: From Approximate to Exact Lifted Probabilistic Inference

We propose an approach to lifted approximate inference for first-order probabilistic models, such as Markov logic networks. It is based on performing exact lifted inference in a simplified first-order model, which is found by relaxing first-order constraints, and then compensating for the relaxation. These simplified models can be incrementally improved by carefully recovering constraints that have been relaxed, also at the first-order level. This leads to a spectrum of approximations, with lifted belief propagation on one end, and exact lifted inference on the other. We discuss how relaxation, compensation, and recovery can be performed, all at the firstorder level, and show empirically that our approach substantially improves on the approximations of both propositional solvers and lifted belief propagation.