Do Finetti: On Causal Effects for Exchangeable Data

We study causal effect estimation in a setting where the data are not i.i.d. (independent and identically distributed). We focus on exchangeable data satisfying an assumption of independent causal mechanisms. Traditional causal effect estimation frameworks, e.g., relying on structural causal models and do-calculus, are typically limited to i.i.d. data and do not extend to more general exchangeable generative processes, which naturally arise in multi-environment data. To address this gap, we develop a generalized framework for exchangeable data and introduce a truncated factorization formula that facilitates both the identification and estimation of causal effects in our setting. To illustrate potential applications, we introduce a causal P\'olya urn model and demonstrate how intervention propagates effects in exchangeable data settings. Finally, we develop an algorithm that performs simultaneous causal discovery and effect estimation given multi-environment data.

Efficient Algorithms for Bayesian Network Parameter Learning from Incomplete Data

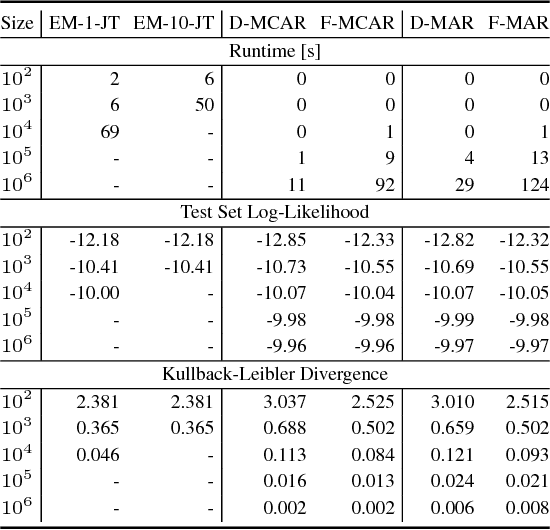
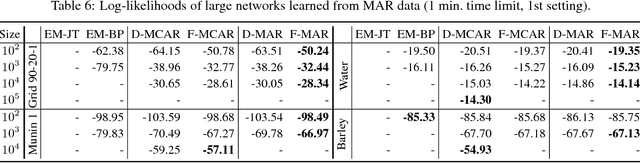
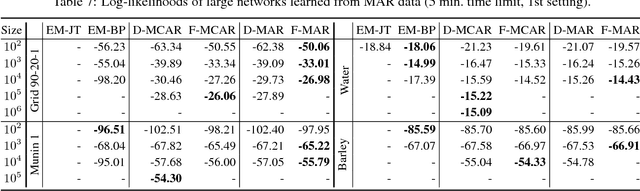
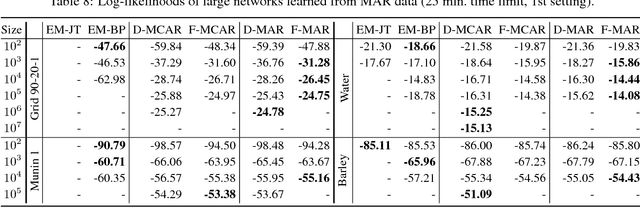
We propose an efficient family of algorithms to learn the parameters of a Bayesian network from incomplete data. In contrast to textbook approaches such as EM and the gradient method, our approach is non-iterative, yields closed form parameter estimates, and eliminates the need for inference in a Bayesian network. Our approach provides consistent parameter estimates for missing data problems that are MCAR, MAR, and in some cases, MNAR. Empirically, our approach is orders of magnitude faster than EM (as our approach requires no inference). Given sufficient data, we learn parameters that can be orders of magnitude more accurate.