Efficient Algorithms for Bayesian Network Parameter Learning from Incomplete Data

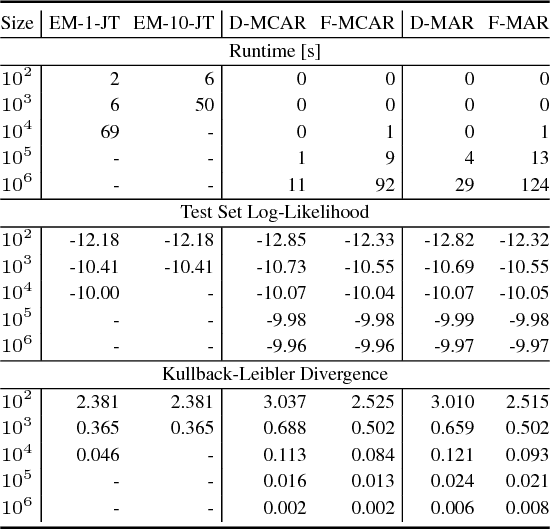
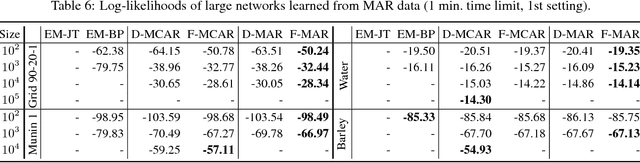
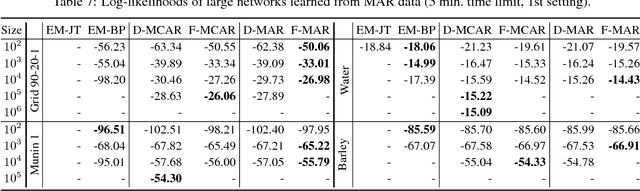
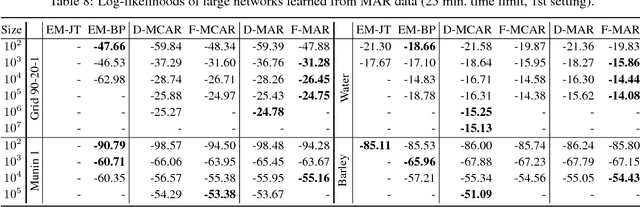
We propose an efficient family of algorithms to learn the parameters of a Bayesian network from incomplete data. In contrast to textbook approaches such as EM and the gradient method, our approach is non-iterative, yields closed form parameter estimates, and eliminates the need for inference in a Bayesian network. Our approach provides consistent parameter estimates for missing data problems that are MCAR, MAR, and in some cases, MNAR. Empirically, our approach is orders of magnitude faster than EM (as our approach requires no inference). Given sufficient data, we learn parameters that can be orders of magnitude more accurate.