Anchal Goyanka
On Symbolically Encoding the Behavior of Random Forests
Jul 03, 2020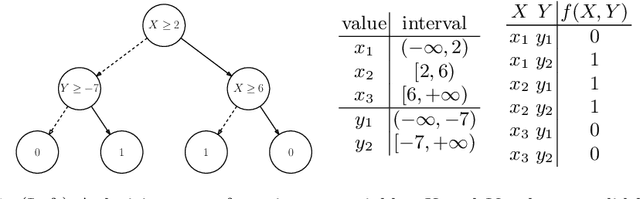
Abstract:Recent work has shown that the input-output behavior of some machine learning systems can be captured symbolically using Boolean expressions or tractable Boolean circuits, which facilitates reasoning about the behavior of these systems. While most of the focus has been on systems with Boolean inputs and outputs, we address systems with discrete inputs and outputs, including ones with discretized continuous variables as in systems based on decision trees. We also focus on the suitability of encodings for computing prime implicants, which have recently played a central role in explaining the decisions of machine learning systems. We show some key distinctions with encodings for satisfiability, and propose an encoding that is sound and complete for the given task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge