SOP-Bench: Complex Industrial SOPs for Evaluating LLM Agents

Large Language Models (LLMs) demonstrate impressive general-purpose reasoning and problem-solving abilities. However, they struggle with executing complex, long-horizon workflows that demand strict adherence to Standard Operating Procedures (SOPs), a critical requirement for real-world industrial automation. Despite this need, there is a lack of public benchmarks that reflect the complexity, structure, and domain-specific nuances of SOPs. To address this, we present three main contributions. First, we introduce a synthetic data generation framework to create realistic, industry-grade SOPs that rigorously test the planning, reasoning, and tool-use capabilities of LLM-based agents. Second, using this framework, we develop SOP-Bench, a benchmark of over 1,800 tasks across 10 industrial domains, each with APIs, tool interfaces, and human-validated test cases. Third, we evaluate two prominent agent architectures: Function-Calling and ReAct Agents, on SOP-Bench, observing average success rates of only 27% and 48%, respectively. Remarkably, when the tool registry is much larger than necessary, agents invoke incorrect tools nearly 100% of the time. These findings underscore a substantial gap between current agentic capabilities of LLMs and the demands of automating real-world SOPs. Performance varies significantly by task and domain, highlighting the need for domain-specific benchmarking and architectural choices before deployment. SOP-Bench is publicly available at http://sop-bench.s3-website-us-west-2.amazonaws.com/. We also release the prompts underpinning the data generation framework to support new domain-specific SOP benchmarks. We invite the community to extend SOP-Bench with SOPs from their industrial domains.

Exponential Convergence of CAVI for Bayesian PCA

Probabilistic principal component analysis (PCA) and its Bayesian variant (BPCA) are widely used for dimension reduction in machine learning and statistics. The main advantage of probabilistic PCA over the traditional formulation is allowing uncertainty quantification. The parameters of BPCA are typically learned using mean-field variational inference, and in particular, the coordinate ascent variational inference (CAVI) algorithm. So far, the convergence speed of CAVI for BPCA has not been characterized. In our paper, we fill this gap in the literature. Firstly, we prove a precise exponential convergence result in the case where the model uses a single principal component (PC). Interestingly, this result is established through a connection with the classical $\textit{power iteration algorithm}$ and it indicates that traditional PCA is retrieved as points estimates of the BPCA parameters. Secondly, we leverage recent tools to prove exponential convergence of CAVI for the model with any number of PCs, thus leading to a more general result, but one that is of a slightly different flavor. To prove the latter result, we additionally needed to introduce a novel lower bound for the symmetric Kullback--Leibler divergence between two multivariate normal distributions, which, we believe, is of independent interest in information theory.

On the Consistency of Maximum Likelihood Estimation of Probabilistic Principal Component Analysis

Probabilistic principal component analysis (PPCA) is currently one of the most used statistical tools to reduce the ambient dimension of the data. From multidimensional scaling to the imputation of missing data, PPCA has a broad spectrum of applications ranging from science and engineering to quantitative finance. Despite this wide applicability in various fields, hardly any theoretical guarantees exist to justify the soundness of the maximal likelihood (ML) solution for this model. In fact, it is well known that the maximum likelihood estimation (MLE) can only recover the true model parameters up to a rotation. The main obstruction is posed by the inherent identifiability nature of the PPCA model resulting from the rotational symmetry of the parameterization. To resolve this ambiguity, we propose a novel approach using quotient topological spaces and in particular, we show that the maximum likelihood solution is consistent in an appropriate quotient Euclidean space. Furthermore, our consistency results encompass a more general class of estimators beyond the MLE. Strong consistency of the ML estimate and consequently strong covariance estimation of the PPCA model have also been established under a compactness assumption.

Measuring and Mitigating Local Instability in Deep Neural Networks

Deep Neural Networks (DNNs) are becoming integral components of real world services relied upon by millions of users. Unfortunately, architects of these systems can find it difficult to ensure reliable performance as irrelevant details like random initialization can unexpectedly change the outputs of a trained system with potentially disastrous consequences. We formulate the model stability problem by studying how the predictions of a model change, even when it is retrained on the same data, as a consequence of stochasticity in the training process. For Natural Language Understanding (NLU) tasks, we find instability in predictions for a significant fraction of queries. We formulate principled metrics, like per-sample ``label entropy'' across training runs or within a single training run, to quantify this phenomenon. Intriguingly, we find that unstable predictions do not appear at random, but rather appear to be clustered in data-specific ways. We study data-agnostic regularization methods to improve stability and propose new data-centric methods that exploit our local stability estimates. We find that our localized data-specific mitigation strategy dramatically outperforms data-agnostic methods, and comes within 90% of the gold standard, achieved by ensembling, at a fraction of the computational cost

Fair-Net: A Network Architecture For Reducing Performance Disparity Between Identifiable Sub-Populations

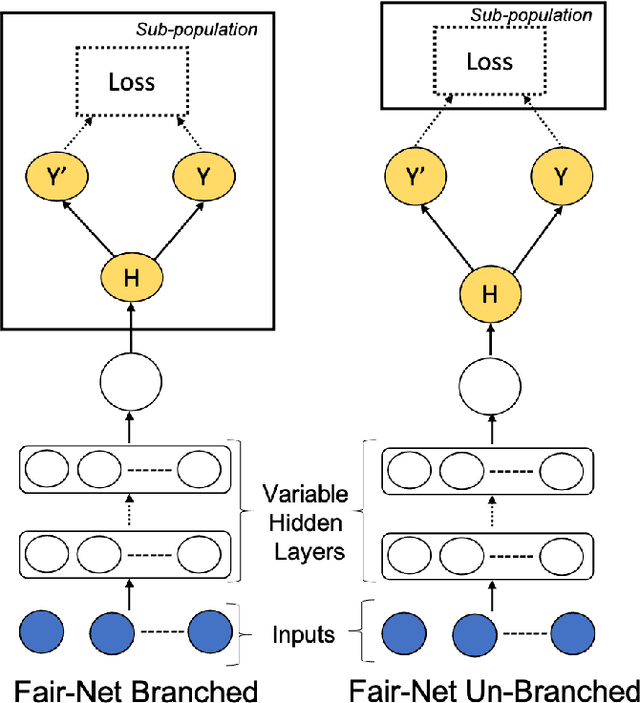
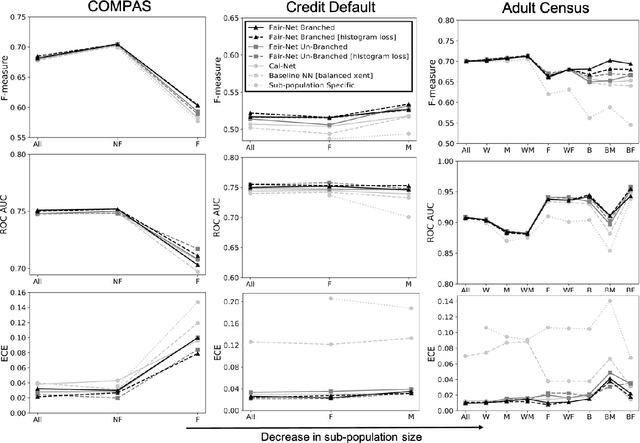
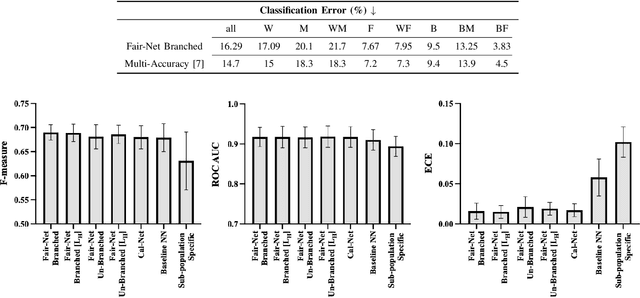
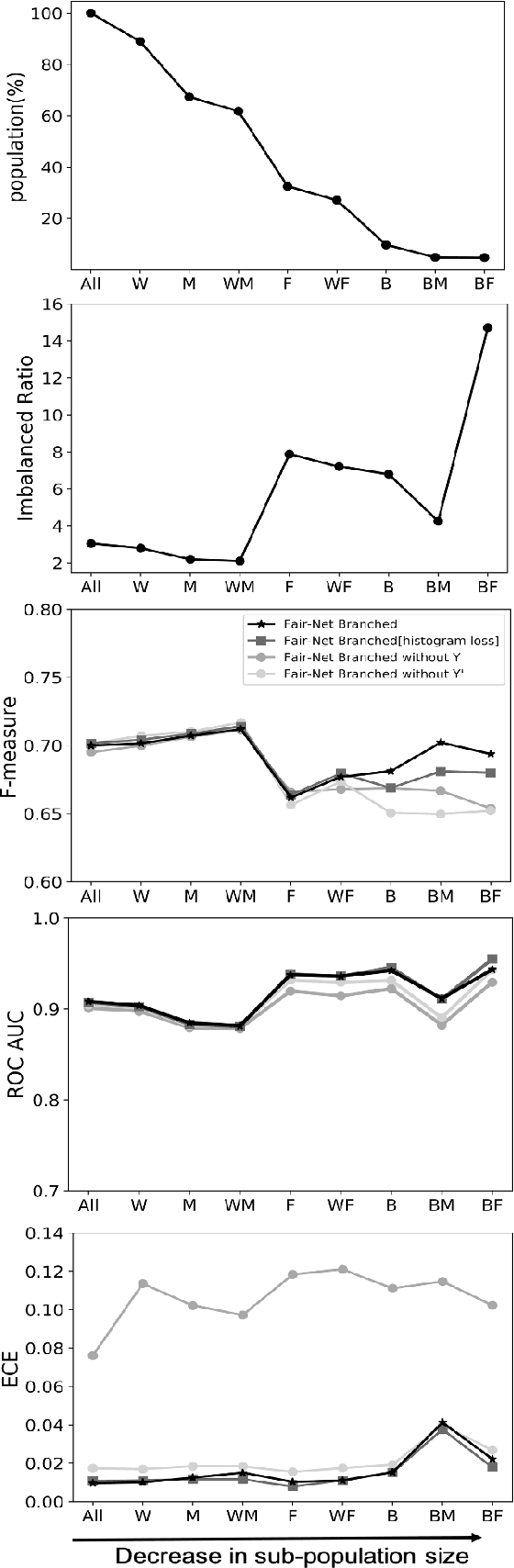
In real world datasets, particular groups are under-represented, much rarer than others, and machine learning classifiers will often preform worse on under-represented populations. This problem is aggravated across many domains where datasets are class imbalanced, with a minority class far rarer than the majority class. Naive approaches to handle under-representation and class imbalance include training sub-population specific classifiers that handle class imbalance or training a global classifier that overlooks sub-population disparities and aims to achieve high overall accuracy by handling class imbalance. In this study, we find that these approaches are vulnerable in class imbalanced datasets with minority sub-populations. We introduced Fair-Net, a branched multitask neural network architecture that improves both classification accuracy and probability calibration across identifiable sub-populations in class imbalanced datasets. Fair-Nets is a straightforward extension to the output layer and error function of a network, so can be incorporated in far more complex architectures. Empirical studies with three real world benchmark datasets demonstrate that Fair-Net improves classification and calibration performance, substantially reducing performance disparity between gender and racial sub-populations.

Deep learning long-range information in undirected graphs with wave networks

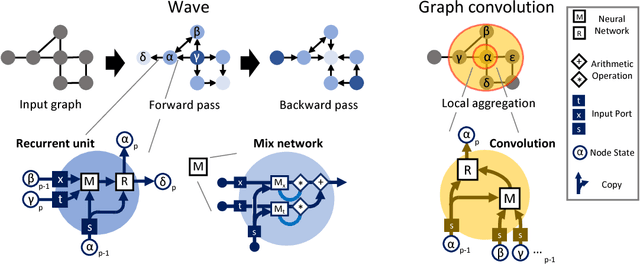
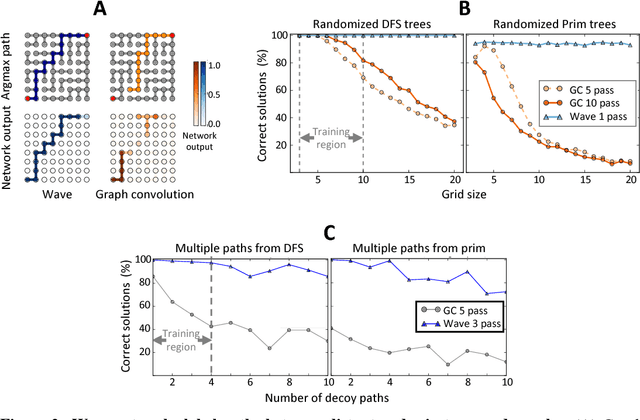
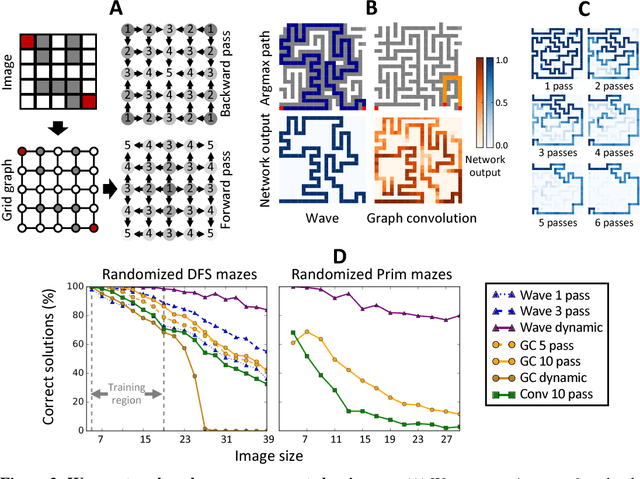
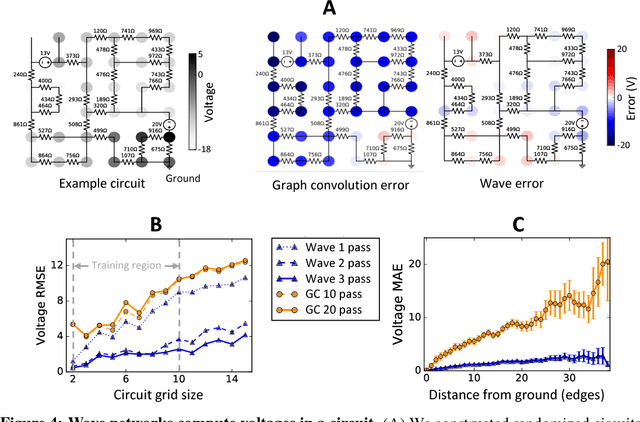
Graph algorithms are key tools in many fields of science and technology. Some of these algorithms depend on propagating information between distant nodes in a graph. Recently, there have been a number of deep learning architectures proposed to learn on undirected graphs. However, most of these architectures aggregate information in the local neighborhood of a node, and therefore they may not be capable of efficiently propagating long-range information. To solve this problem we examine a recently proposed architecture, wave, which propagates information back and forth across an undirected graph in waves of nonlinear computation. We compare wave to graph convolution, an architecture based on local aggregation, and find that wave learns three different graph-based tasks with greater efficiency and accuracy. These three tasks include (1) labeling a path connecting two nodes in a graph, (2) solving a maze presented as an image, and (3) computing voltages in a circuit. These tasks range from trivial to very difficult, but wave can extrapolate from small training examples to much larger testing examples. These results show that wave may be able to efficiently solve a wide range of problems that require long-range information propagation across undirected graphs. An implementation of the wave network, and example code for the maze problem are included in the tflon deep learning toolkit (https://bitbucket.org/mkmatlock/tflon).