PerfDojo: Automated ML Library Generation for Heterogeneous Architectures

The increasing complexity of machine learning models and the proliferation of diverse hardware architectures (CPUs, GPUs, accelerators) make achieving optimal performance a significant challenge. Heterogeneity in instruction sets, specialized kernel requirements for different data types and model features (e.g., sparsity, quantization), and architecture-specific optimizations complicate performance tuning. Manual optimization is resource-intensive, while existing automatic approaches often rely on complex hardware-specific heuristics and uninterpretable intermediate representations, hindering performance portability. We introduce PerfLLM, a novel automatic optimization methodology leveraging Large Language Models (LLMs) and Reinforcement Learning (RL). Central to this is PerfDojo, an environment framing optimization as an RL game using a human-readable, mathematically-inspired code representation that guarantees semantic validity through transformations. This allows effective optimization without prior hardware knowledge, facilitating both human analysis and RL agent training. We demonstrate PerfLLM's ability to achieve significant performance gains across diverse CPU (x86, Arm, RISC-V) and GPU architectures.

VENOM: A Vectorized N:M Format for Unleashing the Power of Sparse Tensor Cores

The increasing success and scaling of Deep Learning models demands higher computational efficiency and power. Sparsification can lead to both smaller models as well as higher compute efficiency, and accelerated hardware is becoming available. However, exploiting it efficiently requires kernel implementations, pruning algorithms, and storage formats, to utilize hardware support of specialized sparse vector units. An example of those are the NVIDIA's Sparse Tensor Cores (SPTCs), which promise a 2x speedup. However, SPTCs only support the 2:4 format, limiting achievable sparsity ratios to 50%. We present the V:N:M format, which enables the execution of arbitrary N:M ratios on SPTCs. To efficiently exploit the resulting format, we propose Spatha, a high-performance sparse-library for DL routines. We show that Spatha achieves up to 37x speedup over cuBLAS. We also demonstrate a second-order pruning technique that enables sparsification to high sparsity ratios with V:N:M and little to no loss in accuracy in modern transformers.

Cached Operator Reordering: A Unified View for Fast GNN Training

Graph Neural Networks (GNNs) are a powerful tool for handling structured graph data and addressing tasks such as node classification, graph classification, and clustering. However, the sparse nature of GNN computation poses new challenges for performance optimization compared to traditional deep neural networks. We address these challenges by providing a unified view of GNN computation, I/O, and memory. By analyzing the computational graphs of the Graph Convolutional Network (GCN) and Graph Attention (GAT) layers -- two widely used GNN layers -- we propose alternative computation strategies. We present adaptive operator reordering with caching, which achieves a speedup of up to 2.43x for GCN compared to the current state-of-the-art. Furthermore, an exploration of different caching schemes for GAT yields a speedup of up to 1.94x. The proposed optimizations save memory, are easily implemented across various hardware platforms, and have the potential to alleviate performance bottlenecks in training large-scale GNN models.

TMPNN: High-Order Polynomial Regression Based on Taylor Map Factorization

Polynomial regression is widely used and can help to express nonlinear patterns. However, considering very high polynomial orders may lead to overfitting and poor extrapolation ability for unseen data. The paper presents a method for constructing a high-order polynomial regression based on the Taylor map factorization. This method naturally implements multi-target regression and can capture internal relationships between targets. Additionally, we introduce an approach for model interpretation in the form of systems of differential equations. By benchmarking on UCI open access datasets, Feynman symbolic regression datasets, and Friedman-1 datasets, we demonstrate that the proposed method performs comparable to the state-of-the-art regression methods and outperforms them on specific tasks.

STen: Productive and Efficient Sparsity in PyTorch

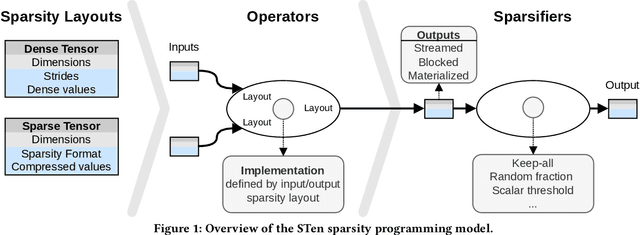
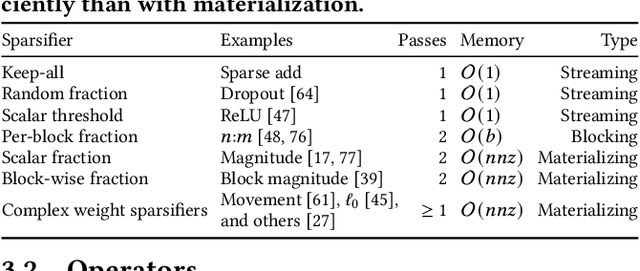
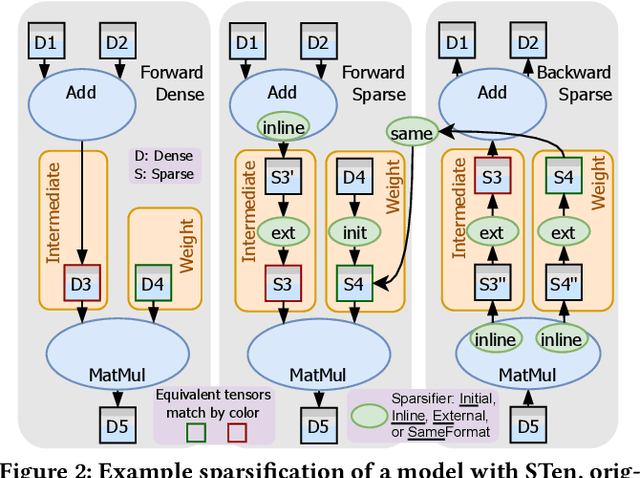
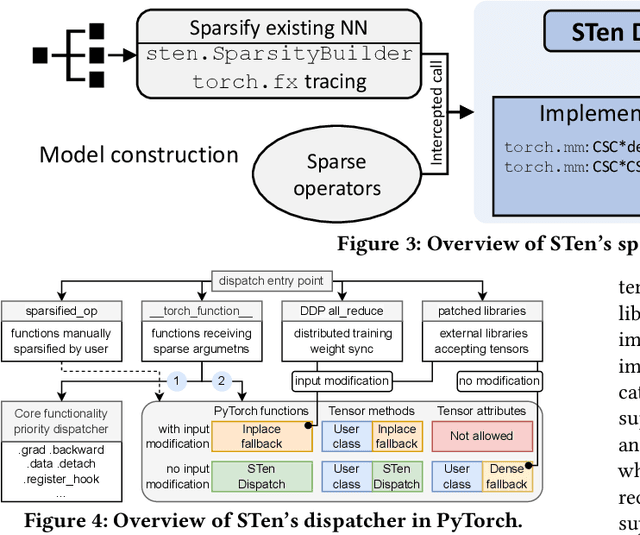
As deep learning models grow, sparsity is becoming an increasingly critical component of deep neural networks, enabling improved performance and reduced storage. However, existing frameworks offer poor support for sparsity. Specialized sparsity engines focus exclusively on sparse inference, while general frameworks primarily focus on sparse tensors in classical formats and neglect the broader sparsification pipeline necessary for using sparse models, especially during training. Further, existing frameworks are not easily extensible: adding a new sparse tensor format or operator is challenging and time-consuming. To address this, we propose STen, a sparsity programming model and interface for PyTorch, which incorporates sparsity layouts, operators, and sparsifiers, in an efficient, customizable, and extensible framework that supports virtually all sparsification methods. We demonstrate this by developing a high-performance grouped n:m sparsity layout for CPU inference at moderate sparsity. STen brings high performance and ease of use to the ML community, making sparsity easily accessible.

A Data-Centric Optimization Framework for Machine Learning

Rapid progress in deep learning is leading to a diverse set of quickly changing models, with a dramatically growing demand for compute. However, as frameworks specialize optimization to patterns in popular networks, they implicitly constrain novel and diverse models that drive progress in research. We empower deep learning researchers by defining a flexible and user-customizable pipeline for optimizing training of arbitrary deep neural networks, based on data movement minimization. The pipeline begins with standard networks in PyTorch or ONNX and transforms computation through progressive lowering. We define four levels of general-purpose transformations, from local intra-operator optimizations to global data movement reduction. These operate on a data-centric graph intermediate representation that expresses computation and data movement at all levels of abstraction, including expanding basic operators such as convolutions to their underlying computations. Central to the design is the interactive and introspectable nature of the pipeline. Every part is extensible through a Python API, and can be tuned interactively using a GUI. We demonstrate competitive performance or speedups on ten different networks, with interactive optimizations discovering new opportunities in EfficientNet.

Physics-Based Deep Neural Networks for Beam Dynamics in Charged Particle Accelerators

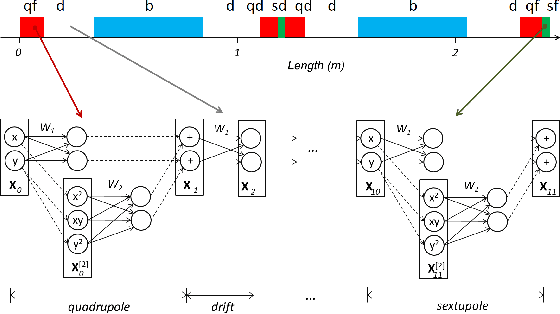
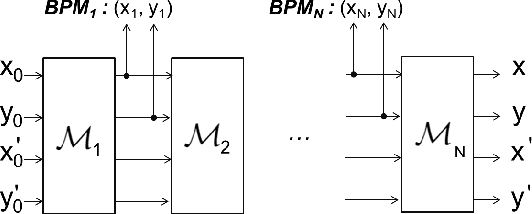
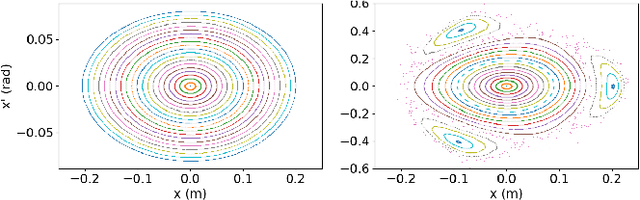
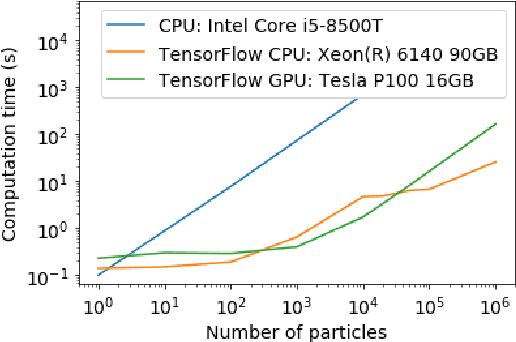
This paper presents a novel approach for constructing neural networks which model charged particle beam dynamics. In our approach, the Taylor maps arising in the representation of dynamics are mapped onto the weights of a polynomial neural network. The resulting network approximates the dynamical system with perfect accuracy prior to training and provides a possibility to tune the network weights on additional experimental data. We propose a symplectic regularization approach for such polynomial neural networks that always restricts the trained model to Hamiltonian systems and significantly improves the training procedure. The proposed networks can be used for beam dynamics simulations or for fine-tuning of beam optics models with experimental data. The structure of the network allows for the modeling of large accelerators with a large number of magnets. We demonstrate our approach on the examples of the existing PETRA III and the planned PETRA IV storage rings at DESY.

Data Movement Is All You Need: A Case Study on Optimizing Transformers

Transformers have become widely used for language modeling and sequence learning tasks, and are one of the most important machine learning workloads today. Training one is a very compute-intensive task, often taking days or weeks, and significant attention has been given to optimizing transformers. Despite this, existing implementations do not efficiently utilize GPUs. We find that data movement is the key bottleneck when training. Due to Amdahl's Law and massive improvements in compute performance, training has now become memory-bound. Further, existing frameworks use suboptimal data layouts. Using these insights, we present a recipe for globally optimizing data movement in transformers. We reduce data movement by up to 22.91% and overall achieve a 1.30x performance improvement over state-of-the-art frameworks when training BERT. Our approach is applicable more broadly to optimizing deep neural networks, and offers insight into how to tackle emerging performance bottlenecks.

Physics-based polynomial neural networks for one-shot learning of dynamical systems from one or a few samples

This paper discusses an approach for incorporating prior physical knowledge into the neural network to improve data efficiency and the generalization of predictive models. If the dynamics of a system approximately follows a given differential equation, the Taylor mapping method can be used to initialize the weights of a polynomial neural network. This allows the fine-tuning of the model from one training sample of real system dynamics. The paper describes practical results on real experiments with both a simple pendulum and one of the largest worldwide X-ray source. It is demonstrated in practice that the proposed approach allows recovering complex physics from noisy, limited, and partial observations and provides meaningful predictions for previously unseen inputs. The approach mainly targets the learning of physical systems when state-of-the-art models are difficult to apply given the lack of training data.

Polynomial Neural Networks and Taylor maps for Dynamical Systems Simulation and Learning

The connection of Taylor maps and polynomial neural networks (PNN) to solve ordinary differential equations (ODEs) numerically is considered. Having the system of ODEs, it is possible to calculate weights of PNN that simulates the dynamics of these equations. It is shown that proposed PNN architecture can provide better accuracy with less computational time in comparison with traditional numerical solvers. Moreover, neural network derived from the ODEs can be used for simulation of system dynamics with different initial conditions, but without training procedure. On the other hand, if the equations are unknown, the weights of the PNN can be fitted in a data-driven way. In the paper we describe the connection of PNN with differential equations in a theoretical way along with the examples for both dynamics simulation and learning with data.