Physics-Based Deep Neural Networks for Beam Dynamics in Charged Particle Accelerators
Paper and Code
Jul 07, 2020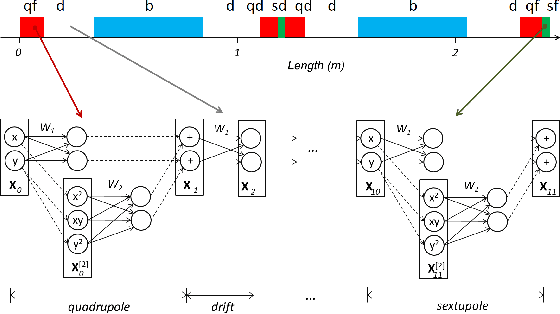
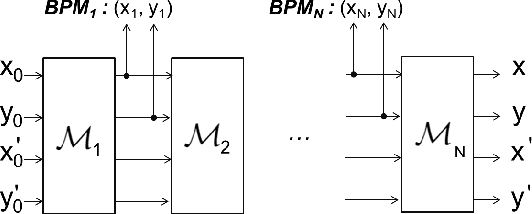
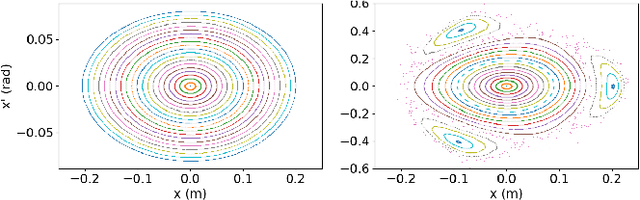
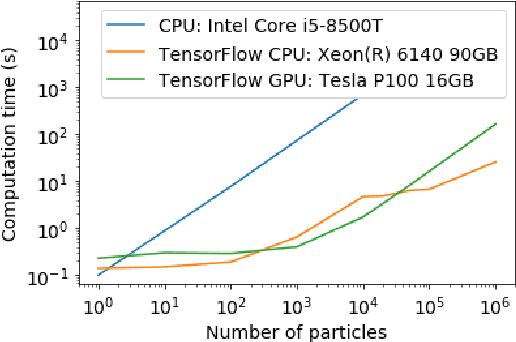
This paper presents a novel approach for constructing neural networks which model charged particle beam dynamics. In our approach, the Taylor maps arising in the representation of dynamics are mapped onto the weights of a polynomial neural network. The resulting network approximates the dynamical system with perfect accuracy prior to training and provides a possibility to tune the network weights on additional experimental data. We propose a symplectic regularization approach for such polynomial neural networks that always restricts the trained model to Hamiltonian systems and significantly improves the training procedure. The proposed networks can be used for beam dynamics simulations or for fine-tuning of beam optics models with experimental data. The structure of the network allows for the modeling of large accelerators with a large number of magnets. We demonstrate our approach on the examples of the existing PETRA III and the planned PETRA IV storage rings at DESY.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge