Formalizing Complex Mathematical Statements with LLMs: A Study on Mathematical Definitions

Thanks to their linguistic capabilities, LLMs offer an opportunity to bridge the gap between informal mathematics and formal languages through autoformalization. However, it is still unclear how well LLMs generalize to sophisticated and naturally occurring mathematical statements. To address this gap, we investigate the task of autoformalizing real-world mathematical definitions -- a critical component of mathematical discourse. Specifically, we introduce two novel resources for autoformalisation, collecting definitions from Wikipedia (Def_Wiki) and arXiv papers (Def_ArXiv). We then systematically evaluate a range of LLMs, analyzing their ability to formalize definitions into Isabelle/HOL. Furthermore, we investigate strategies to enhance LLMs' performance including refinement through external feedback from Proof Assistants, and formal definition grounding, where we guide LLMs through relevant contextual elements from formal mathematical libraries. Our findings reveal that definitions present a greater challenge compared to existing benchmarks, such as miniF2F. In particular, we found that LLMs still struggle with self-correction, and aligning with relevant mathematical libraries. At the same time, structured refinement methods and definition grounding strategies yield notable improvements of up to 16% on self-correction capabilities and 43% on the reduction of undefined errors, highlighting promising directions for enhancing LLM-based autoformalization in real-world scenarios.

Integrating Expert Knowledge into Logical Programs via LLMs

This paper introduces ExKLoP, a novel framework designed to evaluate how effectively Large Language Models (LLMs) integrate expert knowledge into logical reasoning systems. This capability is especially valuable in engineering, where expert knowledge-such as manufacturer-recommended operational ranges-can be directly embedded into automated monitoring systems. By mirroring expert verification steps, tasks like range checking and constraint validation help ensure system safety and reliability. Our approach systematically evaluates LLM-generated logical rules, assessing both syntactic fluency and logical correctness in these critical validation tasks. We also explore the models capacity for self-correction via an iterative feedback loop based on code execution outcomes. ExKLoP presents an extensible dataset comprising 130 engineering premises, 950 prompts, and corresponding validation points. It enables comprehensive benchmarking while allowing control over task complexity and scalability of experiments. We leverage the synthetic data creation methodology to conduct extensive empirical evaluation on a diverse set of LLMs including Llama3, Gemma, Mixtral, Mistral, and Qwen. Results reveal that while models generate nearly perfect syntactically correct code, they frequently exhibit logical errors in translating expert knowledge. Furthermore, iterative self-correction yields only marginal improvements (up to 3%). Overall, ExKLoP serves as a robust evaluation platform that streamlines the selection of effective models for self-correcting systems while clearly delineating the types of errors encountered. The complete implementation, along with all relevant data, is available at GitHub.

Diffusion Twigs with Loop Guidance for Conditional Graph Generation

We introduce a novel score-based diffusion framework named Twigs that incorporates multiple co-evolving flows for enriching conditional generation tasks. Specifically, a central or trunk diffusion process is associated with a primary variable (e.g., graph structure), and additional offshoot or stem processes are dedicated to dependent variables (e.g., graph properties or labels). A new strategy, which we call loop guidance, effectively orchestrates the flow of information between the trunk and the stem processes during sampling. This approach allows us to uncover intricate interactions and dependencies, and unlock new generative capabilities. We provide extensive experiments to demonstrate strong performance gains of the proposed method over contemporary baselines in the context of conditional graph generation, underscoring the potential of Twigs in challenging generative tasks such as inverse molecular design and molecular optimization.

SylloBio-NLI: Evaluating Large Language Models on Biomedical Syllogistic Reasoning

Syllogistic reasoning is crucial for Natural Language Inference (NLI). This capability is particularly significant in specialized domains such as biomedicine, where it can support automatic evidence interpretation and scientific discovery. This paper presents SylloBio-NLI, a novel framework that leverages external ontologies to systematically instantiate diverse syllogistic arguments for biomedical NLI. We employ SylloBio-NLI to evaluate Large Language Models (LLMs) on identifying valid conclusions and extracting supporting evidence across 28 syllogistic schemes instantiated with human genome pathways. Extensive experiments reveal that biomedical syllogistic reasoning is particularly challenging for zero-shot LLMs, which achieve an average accuracy between 70% on generalized modus ponens and 23% on disjunctive syllogism. At the same time, we found that few-shot prompting can boost the performance of different LLMs, including Gemma (+14%) and LLama-3 (+43%). However, a deeper analysis shows that both techniques exhibit high sensitivity to superficial lexical variations, highlighting a dependency between reliability, models' architecture, and pre-training regime. Overall, our results indicate that, while in-context examples have the potential to elicit syllogistic reasoning in LLMs, existing models are still far from achieving the robustness and consistency required for safe biomedical NLI applications.

Graph Neural Flows for Unveiling Systemic Interactions Among Irregularly Sampled Time Series

Interacting systems are prevalent in nature. It is challenging to accurately predict the dynamics of the system if its constituent components are analyzed independently. We develop a graph-based model that unveils the systemic interactions of time series observed at irregular time points, by using a directed acyclic graph to model the conditional dependencies (a form of causal notation) of the system components and learning this graph in tandem with a continuous-time model that parameterizes the solution curves of ordinary differential equations (ODEs). Our technique, a graph neural flow, leads to substantial enhancements over non-graph-based methods, as well as graph-based methods without the modeling of conditional dependencies. We validate our approach on several tasks, including time series classification and forecasting, to demonstrate its efficacy.

Gem: Gaussian Mixture Model Embeddings for Numerical Feature Distributions

Embeddings are now used to underpin a wide variety of data management tasks, including entity resolution, dataset search and semantic type detection. Such applications often involve datasets with numerical columns, but there has been more emphasis placed on the semantics of categorical data in embeddings than on the distinctive features of numerical data. In this paper, we propose a method called Gem (Gaussian mixture model embeddings) that creates embeddings that build on numerical value distributions from columns. The proposed method specializes a Gaussian Mixture Model (GMM) to identify and cluster columns with similar value distributions. We introduce a signature mechanism that generates a probability matrix for each column, indicating its likelihood of belonging to specific Gaussian components, which can be used for different applications, such as to determine semantic types. Finally, we generate embeddings for three numerical data properties: distributional, statistical, and contextual. Our core method focuses solely on numerical columns without using table names or neighboring columns for context. However, the method can be combined with other types of evidence, and we later integrate attribute names with the Gaussian embeddings to evaluate the method's contribution to improving overall performance. We compare Gem with several baseline methods for numeric only and numeric + context tasks, showing that Gem consistently outperforms the baselines on four benchmark datasets.

Consistent Autoformalization for Constructing Mathematical Libraries

Autoformalization is the task of automatically translating mathematical content written in natural language to a formal language expression. The growing language interpretation capabilities of Large Language Models (LLMs), including in formal languages, are lowering the barriers for autoformalization. However, LLMs alone are not capable of consistently and reliably delivering autoformalization, in particular as the complexity and specialization of the target domain grows. As the field evolves into the direction of systematically applying autoformalization towards large mathematical libraries, the need to improve syntactic, terminological and semantic control increases. This paper proposes the coordinated use of three mechanisms, most-similar retrieval augmented generation (MS-RAG), denoising steps, and auto-correction with syntax error feedback (Auto-SEF) to improve autoformalization quality. The empirical analysis, across different models, demonstrates that these mechanisms can deliver autoformalizaton results which are syntactically, terminologically and semantically more consistent. These mechanisms can be applied across different LLMs and have shown to deliver improve results across different model types.

An LLM-based Knowledge Synthesis and Scientific Reasoning Framework for Biomedical Discovery

We present BioLunar, developed using the Lunar framework, as a tool for supporting biological analyses, with a particular emphasis on molecular-level evidence enrichment for biomarker discovery in oncology. The platform integrates Large Language Models (LLMs) to facilitate complex scientific reasoning across distributed evidence spaces, enhancing the capability for harmonizing and reasoning over heterogeneous data sources. Demonstrating its utility in cancer research, BioLunar leverages modular design, reusable data access and data analysis components, and a low-code user interface, enabling researchers of all programming levels to construct LLM-enabled scientific workflows. By facilitating automatic scientific discovery and inference from heterogeneous evidence, BioLunar exemplifies the potential of the integration between LLMs, specialised databases and biomedical tools to support expert-level knowledge synthesis and discovery.

Transformer Normalisation Layers and the Independence of Semantic Subspaces

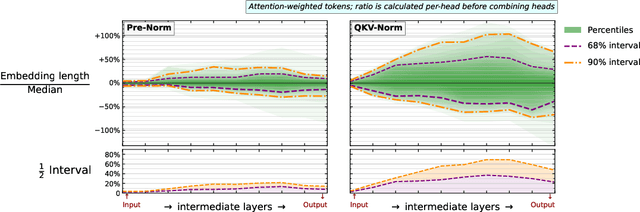
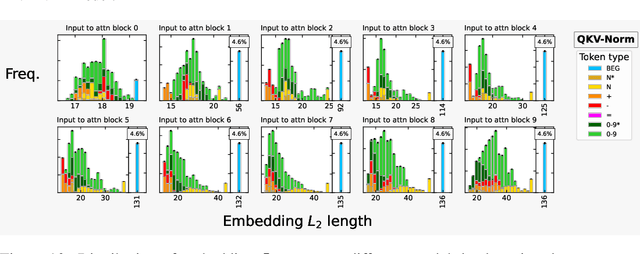
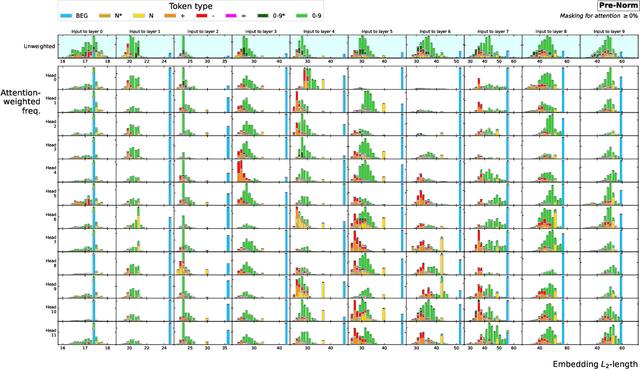
Recent works have shown that transformers can solve contextual reasoning tasks by internally executing computational graphs called circuits. Circuits often use attention to logically match information from subspaces of the representation, e.g. using position-in-sequence to identify the previous token. In this work, we consider a semantic subspace to be any independent subspace of the latent representation that can fully determine an attention distribution. We show that Pre-Norm, the placement of normalisation layer used by state-of-the-art transformers, violates this ability unless the model learns a strict representation structure of orthogonal spheres. This is because it causes linear subspaces to interfere through their common normalisation factor. Theoretically, we analyse circuit stability by modelling this interference as random noise on the $L_2$-norms of the query/key/value vectors, predicting a phenomenon of circuit collapse when sparse-attention shifts to a different token. Empirically, we investigate the sensitivity of real-world models trained for mathematical addition, observing a 1% rate of circuit collapse when the norms are artificially perturbed by $\lesssim$10%. We contrast Pre-Norm with QKV-Norm, which places normalisation after the attention head's linear operators. Theoretically this relaxes the representational constraints. Empirically we observe comparable in-distribution but worse out-of-distribution performance.

Exploring the Limits of Fine-grained LLM-based Physics Inference via Premise Removal Interventions

Language models can hallucinate when performing complex and detailed mathematical reasoning. Physics provides a rich domain for assessing mathematical reasoning capabilities where physical context imbues the use of symbols which needs to satisfy complex semantics (\textit{e.g.,} units, tensorial order), leading to instances where inference may be algebraically coherent, yet unphysical. In this work, we assess the ability of Language Models (LMs) to perform fine-grained mathematical and physical reasoning using a curated dataset encompassing multiple notations and Physics subdomains. We improve zero-shot scores using synthetic in-context examples, and demonstrate non-linear degradation of derivation quality with perturbation strength via the progressive omission of supporting premises. We find that the models' mathematical reasoning is not physics-informed in this setting, where physical context is predominantly ignored in favour of reverse-engineering solutions.