Transformer Normalisation Layers and the Independence of Semantic Subspaces

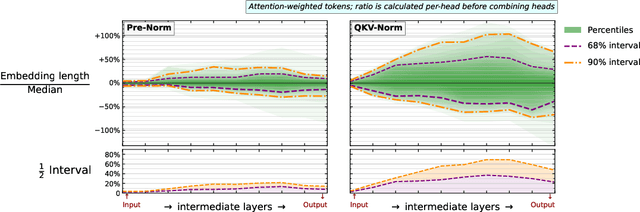
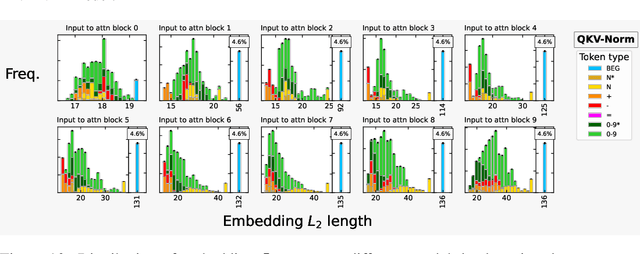
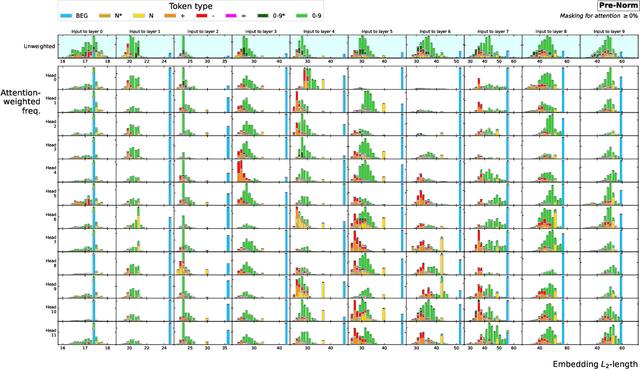
Recent works have shown that transformers can solve contextual reasoning tasks by internally executing computational graphs called circuits. Circuits often use attention to logically match information from subspaces of the representation, e.g. using position-in-sequence to identify the previous token. In this work, we consider a semantic subspace to be any independent subspace of the latent representation that can fully determine an attention distribution. We show that Pre-Norm, the placement of normalisation layer used by state-of-the-art transformers, violates this ability unless the model learns a strict representation structure of orthogonal spheres. This is because it causes linear subspaces to interfere through their common normalisation factor. Theoretically, we analyse circuit stability by modelling this interference as random noise on the $L_2$-norms of the query/key/value vectors, predicting a phenomenon of circuit collapse when sparse-attention shifts to a different token. Empirically, we investigate the sensitivity of real-world models trained for mathematical addition, observing a 1% rate of circuit collapse when the norms are artificially perturbed by $\lesssim$10%. We contrast Pre-Norm with QKV-Norm, which places normalisation after the attention head's linear operators. Theoretically this relaxes the representational constraints. Empirically we observe comparable in-distribution but worse out-of-distribution performance.