WERank: Towards Rank Degradation Prevention for Self-Supervised Learning Using Weight Regularization

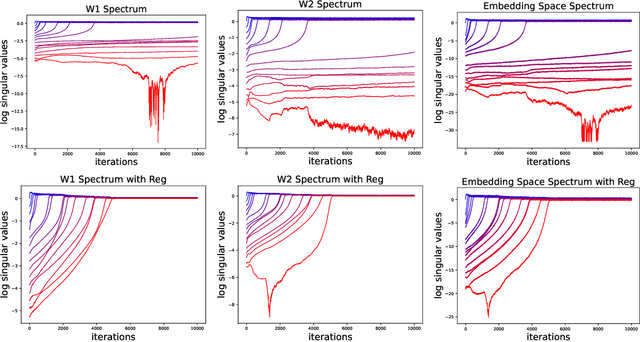
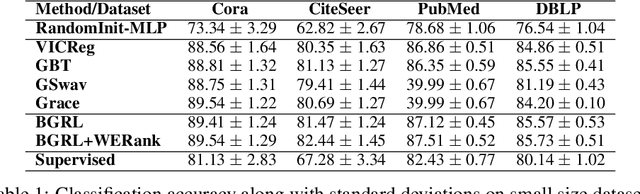
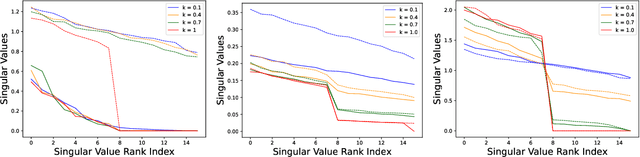
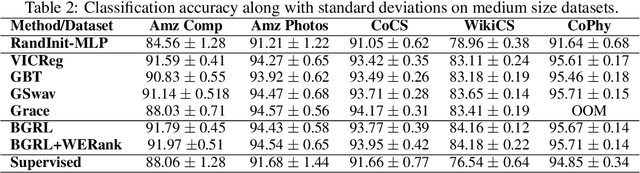
A common phenomena confining the representation quality in Self-Supervised Learning (SSL) is dimensional collapse (also known as rank degeneration), where the learned representations are mapped to a low dimensional subspace of the representation space. The State-of-the-Art SSL methods have shown to suffer from dimensional collapse and fall behind maintaining full rank. Recent approaches to prevent this problem have proposed using contrastive losses, regularization techniques, or architectural tricks. We propose WERank, a new regularizer on the weight parameters of the network to prevent rank degeneration at different layers of the network. We provide empirical evidence and mathematical justification to demonstrate the effectiveness of the proposed regularization method in preventing dimensional collapse. We verify the impact of WERank on graph SSL where dimensional collapse is more pronounced due to the lack of proper data augmentation. We empirically demonstrate that WERank is effective in helping BYOL to achieve higher rank during SSL pre-training and consequently downstream accuracy during evaluation probing. Ablation studies and experimental analysis shed lights on the underlying factors behind the performance gains of the proposed approach.

Scalable Graph Self-Supervised Learning

In regularization Self-Supervised Learning (SSL) methods for graphs, computational complexity increases with the number of nodes in graphs and embedding dimensions. To mitigate the scalability of non-contrastive graph SSL, we propose a novel approach to reduce the cost of computing the covariance matrix for the pre-training loss function with volume-maximization terms. Our work focuses on reducing the cost associated with the loss computation via graph node or dimension sampling. We provide theoretical insight into why dimension sampling would result in accurate loss computations and support it with mathematical derivation of the novel approach. We develop our experimental setup on the node-level graph prediction tasks, where SSL pre-training has shown to be difficult due to the large size of real world graphs. Our experiments demonstrate that the cost associated with the loss computation can be reduced via node or dimension sampling without lowering the downstream performance. Our results demonstrate that sampling mostly results in improved downstream performance. Ablation studies and experimental analysis are provided to untangle the role of the different factors in the experimental setup.

Pro-KD: Progressive Distillation by Following the Footsteps of the Teacher

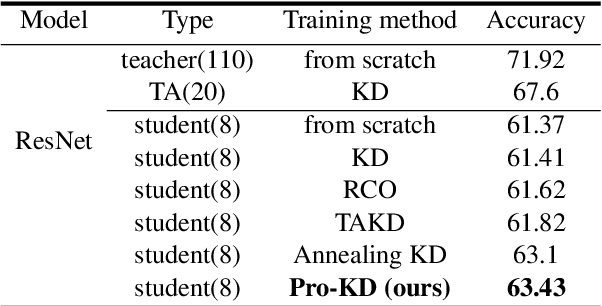
With ever growing scale of neural models, knowledge distillation (KD) attracts more attention as a prominent tool for neural model compression. However, there are counter intuitive observations in the literature showing some challenging limitations of KD. A case in point is that the best performing checkpoint of the teacher might not necessarily be the best teacher for training the student in KD. Therefore, one important question would be how to find the best checkpoint of the teacher for distillation? Searching through the checkpoints of the teacher would be a very tedious and computationally expensive process, which we refer to as the \textit{checkpoint-search problem}. Moreover, another observation is that larger teachers might not necessarily be better teachers in KD which is referred to as the \textit{capacity-gap} problem. To address these challenging problems, in this work, we introduce our progressive knowledge distillation (Pro-KD) technique which defines a smoother training path for the student by following the training footprints of the teacher instead of solely relying on distilling from a single mature fully-trained teacher. We demonstrate that our technique is quite effective in mitigating the capacity-gap problem and the checkpoint search problem. We evaluate our technique using a comprehensive set of experiments on different tasks such as image classification (CIFAR-10 and CIFAR-100), natural language understanding tasks of the GLUE benchmark, and question answering (SQuAD 1.1 and 2.0) using BERT-based models and consistently got superior results over state-of-the-art techniques.

Quantized Fisher Discriminant Analysis

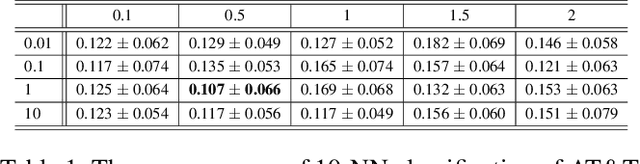
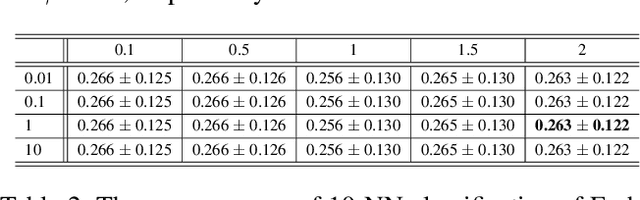
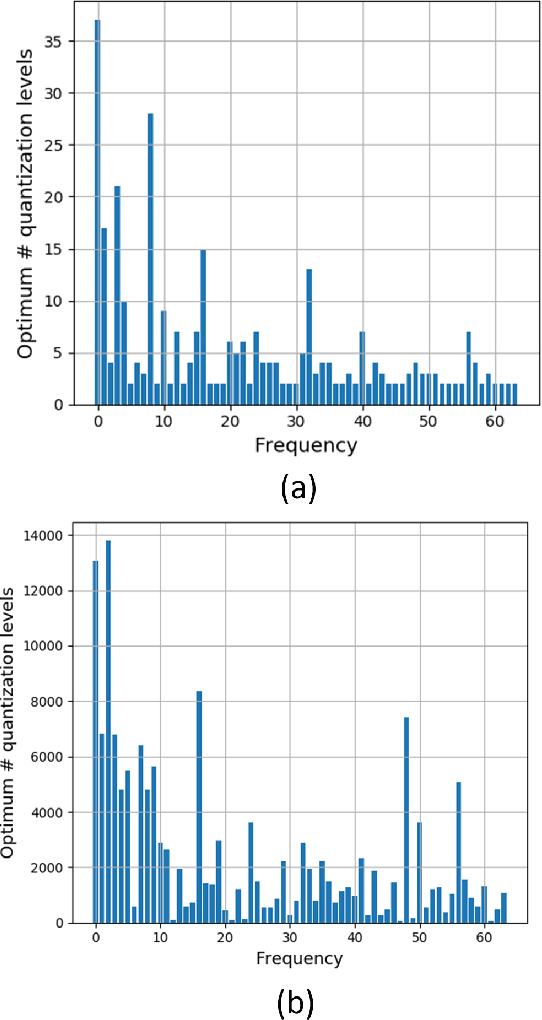
This paper proposes a new subspace learning method, named Quantized Fisher Discriminant Analysis (QFDA), which makes use of both machine learning and information theory. There is a lack of literature for combination of machine learning and information theory and this paper tries to tackle this gap. QFDA finds a subspace which discriminates the uniformly quantized images in the Discrete Cosine Transform (DCT) domain at least as well as discrimination of non-quantized images by Fisher Discriminant Analysis (FDA) while the images have been compressed. This helps the user to throw away the original images and keep the compressed images instead without noticeable loss of classification accuracy. We propose a cost function whose minimization can be interpreted as rate-distortion optimization in information theory. We also propose quantized Fisherfaces for facial analysis in QFDA. Our experiments on AT&T face dataset and Fashion MNIST dataset show the effectiveness of this subspace learning method.