Alexandre de Brébisson
A Cheap Linear Attention Mechanism with Fast Lookups and Fixed-Size Representations
Sep 19, 2016

Abstract:The softmax content-based attention mechanism has proven to be very beneficial in many applications of recurrent neural networks. Nevertheless it suffers from two major computational limitations. First, its computations for an attention lookup scale linearly in the size of the attended sequence. Second, it does not encode the sequence into a fixed-size representation but instead requires to memorize all the hidden states. These two limitations restrict the use of the softmax attention mechanism to relatively small-scale applications with short sequences and few lookups per sequence. In this work we introduce a family of linear attention mechanisms designed to overcome the two limitations listed above. We show that removing the softmax non-linearity from the traditional attention formulation yields constant-time attention lookups and fixed-size representations of the attended sequences. These properties make these linear attention mechanisms particularly suitable for large-scale applications with extreme query loads, real-time requirements and memory constraints. Early experiments on a question answering task show that these linear mechanisms yield significantly better accuracy results than no attention, but obviously worse than their softmax alternative.
Exact gradient updates in time independent of output size for the spherical loss family
Jun 26, 2016



Abstract:An important class of problems involves training deep neural networks with sparse prediction targets of very high dimension D. These occur naturally in e.g. neural language models or the learning of word-embeddings, often posed as predicting the probability of next words among a vocabulary of size D (e.g. 200,000). Computing the equally large, but typically non-sparse D-dimensional output vector from a last hidden layer of reasonable dimension d (e.g. 500) incurs a prohibitive O(Dd) computational cost for each example, as does updating the $D \times d$ output weight matrix and computing the gradient needed for backpropagation to previous layers. While efficient handling of large sparse network inputs is trivial, the case of large sparse targets is not, and has thus so far been sidestepped with approximate alternatives such as hierarchical softmax or sampling-based approximations during training. In this work we develop an original algorithmic approach which, for a family of loss functions that includes squared error and spherical softmax, can compute the exact loss, gradient update for the output weights, and gradient for backpropagation, all in $O(d^{2})$ per example instead of $O(Dd)$, remarkably without ever computing the D-dimensional output. The proposed algorithm yields a speedup of up to $D/4d$ i.e. two orders of magnitude for typical sizes, for that critical part of the computations that often dominates the training time in this kind of network architecture.
The Z-loss: a shift and scale invariant classification loss belonging to the Spherical Family
May 27, 2016



Abstract:Despite being the standard loss function to train multi-class neural networks, the log-softmax has two potential limitations. First, it involves computations that scale linearly with the number of output classes, which can restrict the size of problems we are able to tackle with current hardware. Second, it remains unclear how close it matches the task loss such as the top-k error rate or other non-differentiable evaluation metrics which we aim to optimize ultimately. In this paper, we introduce an alternative classification loss function, the Z-loss, which is designed to address these two issues. Unlike the log-softmax, it has the desirable property of belonging to the spherical loss family (Vincent et al., 2015), a class of loss functions for which training can be performed very efficiently with a complexity independent of the number of output classes. We show experimentally that it significantly outperforms the other spherical loss functions previously investigated. Furthermore, we show on a word language modeling task that it also outperforms the log-softmax with respect to certain ranking scores, such as top-k scores, suggesting that the Z-loss has the flexibility to better match the task loss. These qualities thus makes the Z-loss an appealing candidate to train very efficiently large output networks such as word-language models or other extreme classification problems. On the One Billion Word (Chelba et al., 2014) dataset, we are able to train a model with the Z-loss 40 times faster than the log-softmax and more than 4 times faster than the hierarchical softmax.
Theano: A Python framework for fast computation of mathematical expressions
May 09, 2016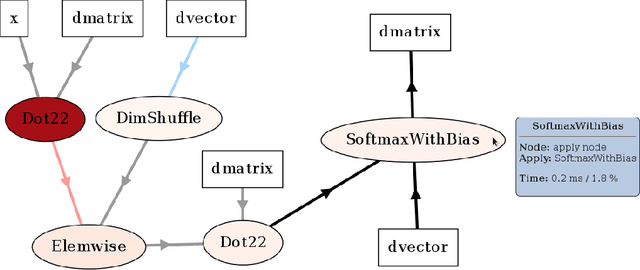
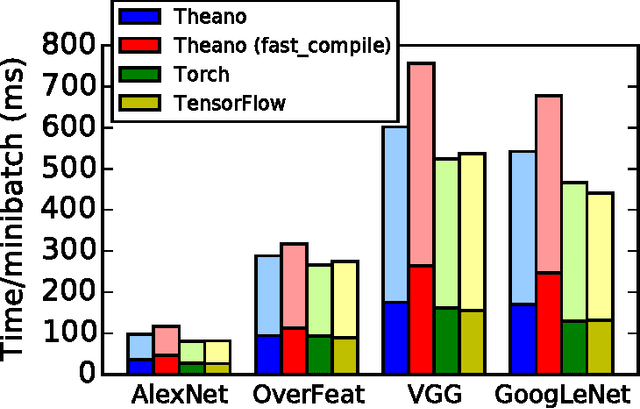
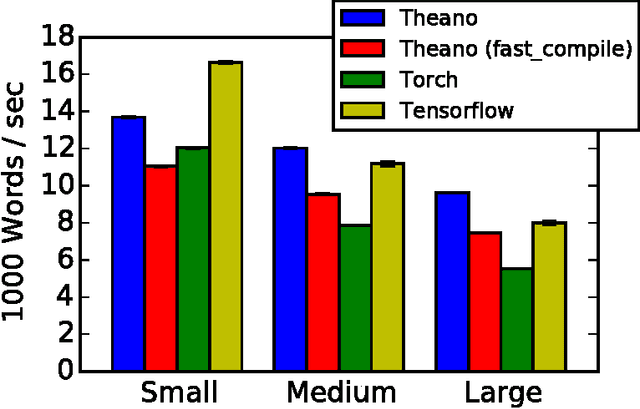
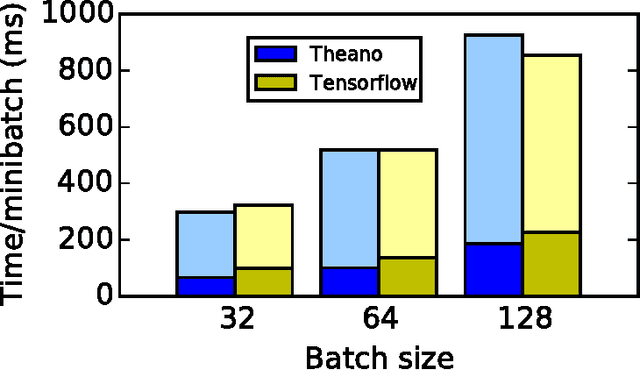
Abstract:Theano is a Python library that allows to define, optimize, and evaluate mathematical expressions involving multi-dimensional arrays efficiently. Since its introduction, it has been one of the most used CPU and GPU mathematical compilers - especially in the machine learning community - and has shown steady performance improvements. Theano is being actively and continuously developed since 2008, multiple frameworks have been built on top of it and it has been used to produce many state-of-the-art machine learning models. The present article is structured as follows. Section I provides an overview of the Theano software and its community. Section II presents the principal features of Theano and how to use them, and compares them with other similar projects. Section III focuses on recently-introduced functionalities and improvements. Section IV compares the performance of Theano against Torch7 and TensorFlow on several machine learning models. Section V discusses current limitations of Theano and potential ways of improving it.
An Exploration of Softmax Alternatives Belonging to the Spherical Loss Family
Feb 28, 2016



Abstract:In a multi-class classification problem, it is standard to model the output of a neural network as a categorical distribution conditioned on the inputs. The output must therefore be positive and sum to one, which is traditionally enforced by a softmax. This probabilistic mapping allows to use the maximum likelihood principle, which leads to the well-known log-softmax loss. However the choice of the softmax function seems somehow arbitrary as there are many other possible normalizing functions. It is thus unclear why the log-softmax loss would perform better than other loss alternatives. In particular Vincent et al. (2015) recently introduced a class of loss functions, called the spherical family, for which there exists an efficient algorithm to compute the updates of the output weights irrespective of the output size. In this paper, we explore several loss functions from this family as possible alternatives to the traditional log-softmax. In particular, we focus our investigation on spherical bounds of the log-softmax loss and on two spherical log-likelihood losses, namely the log-Spherical Softmax suggested by Vincent et al. (2015) and the log-Taylor Softmax that we introduce. Although these alternatives do not yield as good results as the log-softmax loss on two language modeling tasks, they surprisingly outperform it in our experiments on MNIST and CIFAR-10, suggesting that they might be relevant in a broad range of applications.
Artificial Neural Networks Applied to Taxi Destination Prediction
Sep 21, 2015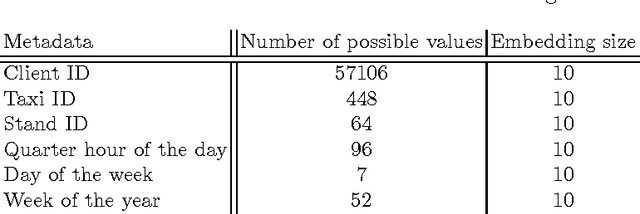
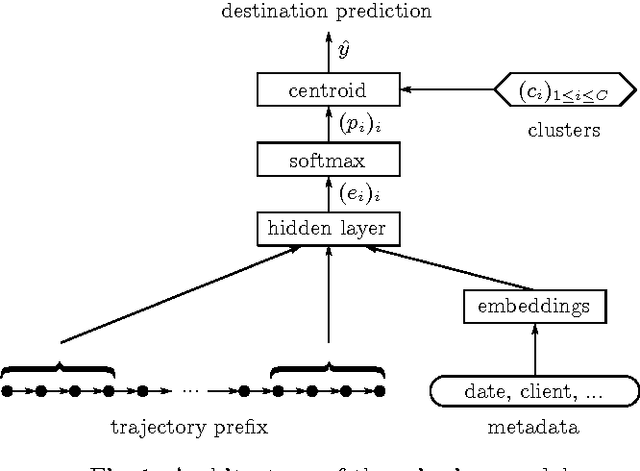

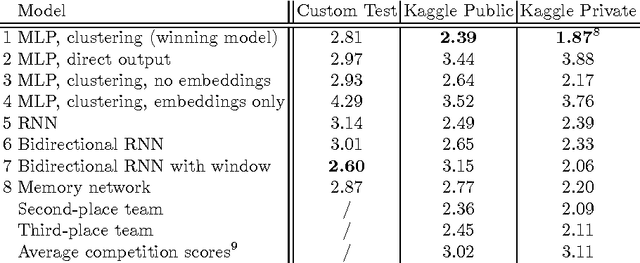
Abstract:We describe our first-place solution to the ECML/PKDD discovery challenge on taxi destination prediction. The task consisted in predicting the destination of a taxi based on the beginning of its trajectory, represented as a variable-length sequence of GPS points, and diverse associated meta-information, such as the departure time, the driver id and client information. Contrary to most published competitor approaches, we used an almost fully automated approach based on neural networks and we ranked first out of 381 teams. The architectures we tried use multi-layer perceptrons, bidirectional recurrent neural networks and models inspired from recently introduced memory networks. Our approach could easily be adapted to other applications in which the goal is to predict a fixed-length output from a variable-length sequence.
Efficient Exact Gradient Update for training Deep Networks with Very Large Sparse Targets
Jul 14, 2015


Abstract:An important class of problems involves training deep neural networks with sparse prediction targets of very high dimension D. These occur naturally in e.g. neural language models or the learning of word-embeddings, often posed as predicting the probability of next words among a vocabulary of size D (e.g. 200 000). Computing the equally large, but typically non-sparse D-dimensional output vector from a last hidden layer of reasonable dimension d (e.g. 500) incurs a prohibitive O(Dd) computational cost for each example, as does updating the D x d output weight matrix and computing the gradient needed for backpropagation to previous layers. While efficient handling of large sparse network inputs is trivial, the case of large sparse targets is not, and has thus so far been sidestepped with approximate alternatives such as hierarchical softmax or sampling-based approximations during training. In this work we develop an original algorithmic approach which, for a family of loss functions that includes squared error and spherical softmax, can compute the exact loss, gradient update for the output weights, and gradient for backpropagation, all in O(d^2) per example instead of O(Dd), remarkably without ever computing the D-dimensional output. The proposed algorithm yields a speedup of D/4d , i.e. two orders of magnitude for typical sizes, for that critical part of the computations that often dominates the training time in this kind of network architecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge