Alex Tong
Online Aggregation of Trajectory Predictors
Feb 11, 2025Abstract:Trajectory prediction, the task of forecasting future agent behavior from past data, is central to safe and efficient autonomous driving. A diverse set of methods (e.g., rule-based or learned with different architectures and datasets) have been proposed, yet it is often the case that the performance of these methods is sensitive to the deployment environment (e.g., how well the design rules model the environment, or how accurately the test data match the training data). Building upon the principled theory of online convex optimization but also going beyond convexity and stationarity, we present a lightweight and model-agnostic method to aggregate different trajectory predictors online. We propose treating each individual trajectory predictor as an "expert" and maintaining a probability vector to mix the outputs of different experts. Then, the key technical approach lies in leveraging online data -the true agent behavior to be revealed at the next timestep- to form a convex-or-nonconvex, stationary-or-dynamic loss function whose gradient steers the probability vector towards choosing the best mixture of experts. We instantiate this method to aggregate trajectory predictors trained on different cities in the NUSCENES dataset and show that it performs just as well, if not better than, any singular model, even when deployed on the out-of-distribution LYFT dataset.
Finding Archetypal Spaces for Data Using Neural Networks
Jan 25, 2019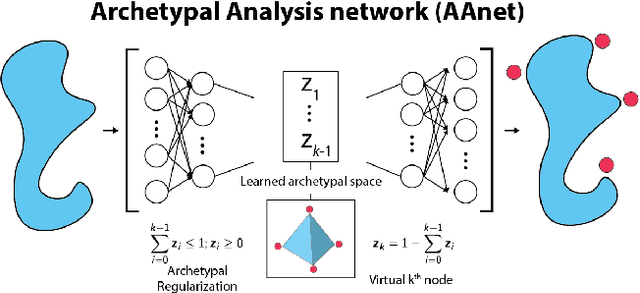
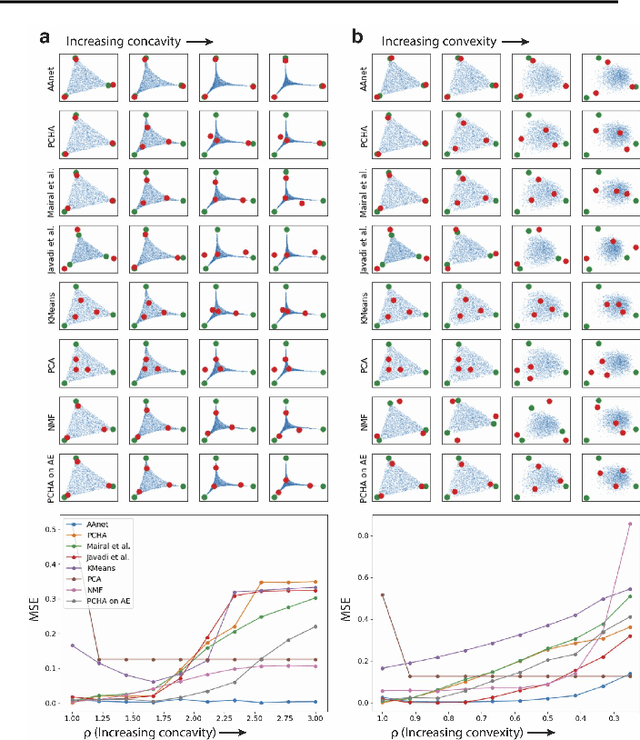
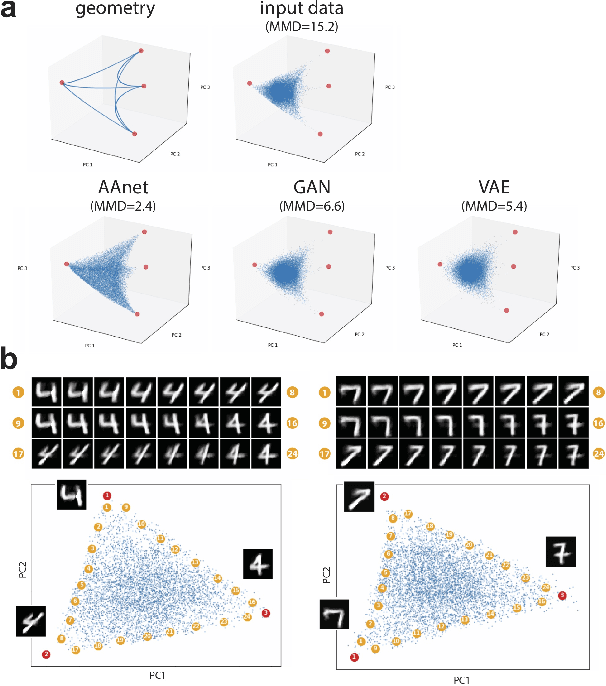
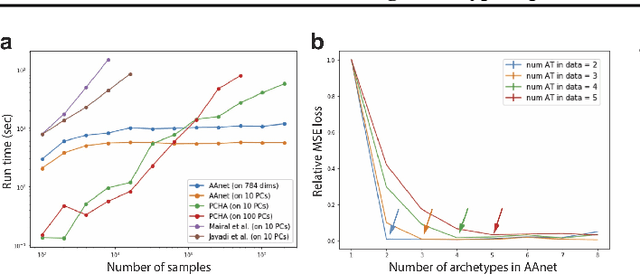
Abstract:Archetypal analysis is a type of factor analysis where data is fit by a convex polytope whose corners are "archetypes" of the data, with the data represented as a convex combination of these archetypal points. While archetypal analysis has been used on biological data, it has not achieved widespread adoption because most data are not well fit by a convex polytope in either the ambient space or after standard data transformations. We propose a new approach to archetypal analysis. Instead of fitting a convex polytope directly on data or after a specific data transformation, we train a neural network (AAnet) to learn a transformation under which the data can best fit into a polytope. We validate this approach on synthetic data where we add nonlinearity. Here, AAnet is the only method that correctly identifies the archetypes. We also demonstrate AAnet on two biological datasets. In a T cell dataset measured with single cell RNA-sequencing, AAnet identifies several archetypal states corresponding to naive, memory, and cytotoxic T cells. In a dataset of gut microbiome profiles, AAnet recovers both previously described microbiome states and identifies novel extrema in the data. Finally, we show that AAnet has generative properties allowing us to uniformly sample from the data geometry even when the input data is not uniformly distributed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge