Finding Archetypal Spaces for Data Using Neural Networks
Paper and Code
Jan 25, 2019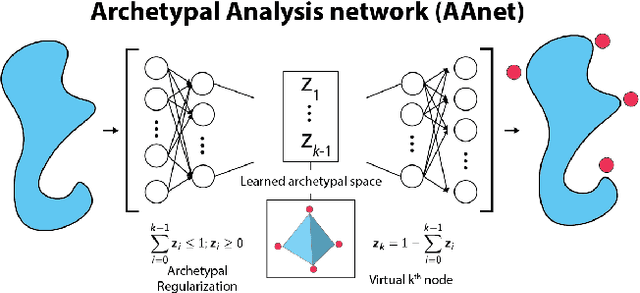
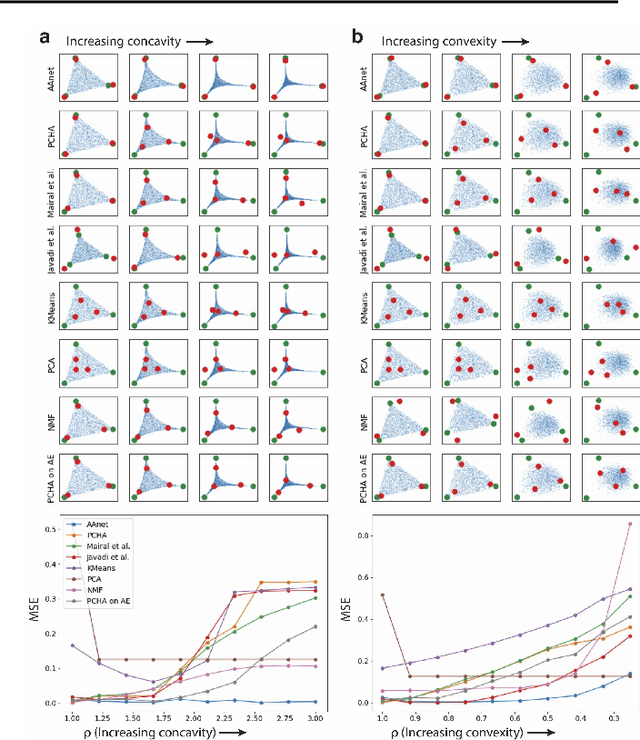
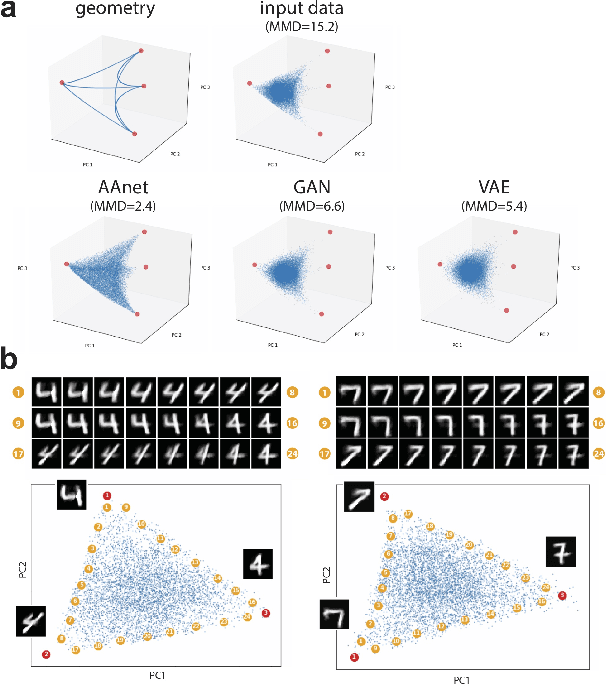
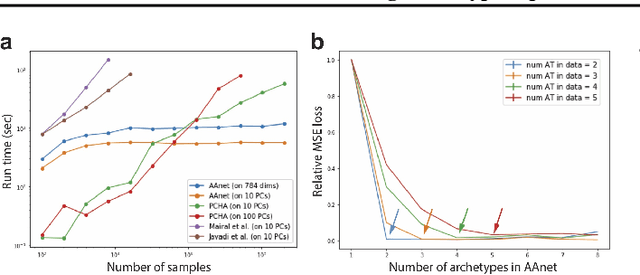
Archetypal analysis is a type of factor analysis where data is fit by a convex polytope whose corners are "archetypes" of the data, with the data represented as a convex combination of these archetypal points. While archetypal analysis has been used on biological data, it has not achieved widespread adoption because most data are not well fit by a convex polytope in either the ambient space or after standard data transformations. We propose a new approach to archetypal analysis. Instead of fitting a convex polytope directly on data or after a specific data transformation, we train a neural network (AAnet) to learn a transformation under which the data can best fit into a polytope. We validate this approach on synthetic data where we add nonlinearity. Here, AAnet is the only method that correctly identifies the archetypes. We also demonstrate AAnet on two biological datasets. In a T cell dataset measured with single cell RNA-sequencing, AAnet identifies several archetypal states corresponding to naive, memory, and cytotoxic T cells. In a dataset of gut microbiome profiles, AAnet recovers both previously described microbiome states and identifies novel extrema in the data. Finally, we show that AAnet has generative properties allowing us to uniformly sample from the data geometry even when the input data is not uniformly distributed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge