The Generative Leap: Sharp Sample Complexity for Efficiently Learning Gaussian Multi-Index Models

In this work we consider generic Gaussian Multi-index models, in which the labels only depend on the (Gaussian) $d$-dimensional inputs through their projection onto a low-dimensional $r = O_d(1)$ subspace, and we study efficient agnostic estimation procedures for this hidden subspace. We introduce the \emph{generative leap} exponent $k^\star$, a natural extension of the generative exponent from [Damian et al.'24] to the multi-index setting. We first show that a sample complexity of $n=\Theta(d^{1 \vee \k/2})$ is necessary in the class of algorithms captured by the Low-Degree-Polynomial framework. We then establish that this sample complexity is also sufficient, by giving an agnostic sequential estimation procedure (that is, requiring no prior knowledge of the multi-index model) based on a spectral U-statistic over appropriate Hermite tensors. We further compute the generative leap exponent for several examples including piecewise linear functions (deep ReLU networks with bias), and general deep neural networks (with $r$-dimensional first hidden layer).

Learning Compositional Functions with Transformers from Easy-to-Hard Data

Transformer-based language models have demonstrated impressive capabilities across a range of complex reasoning tasks. Prior theoretical work exploring the expressive power of transformers has shown that they can efficiently perform multi-step reasoning tasks involving parallelizable computations. However, the learnability of such constructions, particularly the conditions on the data distribution that enable efficient learning via gradient-based optimization, remains an open question. Towards answering this question, in this work we study the learnability of the $k$-fold composition task, which requires computing an interleaved composition of $k$ input permutations and $k$ hidden permutations, and can be expressed by a transformer with $O(\log k)$ layers. On the negative front, we prove a Statistical Query (SQ) lower bound showing that any SQ learner that makes only polynomially-many queries to an SQ oracle for the $k$-fold composition task distribution must have sample size exponential in $k$, thus establishing a statistical-computational gap. On the other hand, we show that this function class can be efficiently learned, with runtime and sample complexity polynomial in $k$, by gradient descent on an $O(\log k)$-depth transformer via two different curriculum learning strategies: one in which data consists of $k'$-fold composition functions with $k' \le k$ presented in increasing difficulty, and another in which all such data is presented simultaneously. Our work sheds light on the necessity and sufficiency of having both easy and hard examples in the data distribution for transformers to learn complex compositional tasks.

Understanding Optimization in Deep Learning with Central Flows

Optimization in deep learning remains poorly understood, even in the simple setting of deterministic (i.e. full-batch) training. A key difficulty is that much of an optimizer's behavior is implicitly determined by complex oscillatory dynamics, referred to as the "edge of stability." The main contribution of this paper is to show that an optimizer's implicit behavior can be explicitly captured by a "central flow:" a differential equation which models the time-averaged optimization trajectory. We show that these flows can empirically predict long-term optimization trajectories of generic neural networks with a high degree of numerical accuracy. By interpreting these flows, we reveal for the first time 1) the precise sense in which RMSProp adapts to the local loss landscape, and 2) an "acceleration via regularization" mechanism, wherein adaptive optimizers implicitly navigate towards low-curvature regions in which they can take larger steps. This mechanism is key to the efficacy of these adaptive optimizers. Overall, we believe that central flows constitute a promising tool for reasoning about optimization in deep learning.

Computational-Statistical Gaps in Gaussian Single-Index Models

Single-Index Models are high-dimensional regression problems with planted structure, whereby labels depend on an unknown one-dimensional projection of the input via a generic, non-linear, and potentially non-deterministic transformation. As such, they encompass a broad class of statistical inference tasks, and provide a rich template to study statistical and computational trade-offs in the high-dimensional regime. While the information-theoretic sample complexity to recover the hidden direction is linear in the dimension $d$, we show that computationally efficient algorithms, both within the Statistical Query (SQ) and the Low-Degree Polynomial (LDP) framework, necessarily require $\Omega(d^{k^\star/2})$ samples, where $k^\star$ is a "generative" exponent associated with the model that we explicitly characterize. Moreover, we show that this sample complexity is also sufficient, by establishing matching upper bounds using a partial-trace algorithm. Therefore, our results provide evidence of a sharp computational-to-statistical gap (under both the SQ and LDP class) whenever $k^\star>2$. To complete the study, we provide examples of smooth and Lipschitz deterministic target functions with arbitrarily large generative exponents $k^\star$.

How Transformers Learn Causal Structure with Gradient Descent

The incredible success of transformers on sequence modeling tasks can be largely attributed to the self-attention mechanism, which allows information to be transferred between different parts of a sequence. Self-attention allows transformers to encode causal structure which makes them particularly suitable for sequence modeling. However, the process by which transformers learn such causal structure via gradient-based training algorithms remains poorly understood. To better understand this process, we introduce an in-context learning task that requires learning latent causal structure. We prove that gradient descent on a simplified two-layer transformer learns to solve this task by encoding the latent causal graph in the first attention layer. The key insight of our proof is that the gradient of the attention matrix encodes the mutual information between tokens. As a consequence of the data processing inequality, the largest entries of this gradient correspond to edges in the latent causal graph. As a special case, when the sequences are generated from in-context Markov chains, we prove that transformers learn an induction head (Olsson et al., 2022). We confirm our theoretical findings by showing that transformers trained on our in-context learning task are able to recover a wide variety of causal structures.

Fine-Tuning Language Models with Just Forward Passes

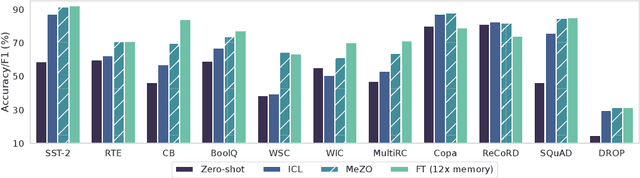
Fine-tuning language models (LMs) has yielded success on diverse downstream tasks, but as LMs grow in size, backpropagation requires a prohibitively large amount of memory. Zeroth-order (ZO) methods can in principle estimate gradients using only two forward passes but are theorized to be catastrophically slow for optimizing large models. In this work, we propose a memory-efficient zerothorder optimizer (MeZO), adapting the classical ZO-SGD method to operate in-place, thereby fine-tuning LMs with the same memory footprint as inference. For example, with a single A100 80GB GPU, MeZO can train a 30-billion parameter model, whereas fine-tuning with backpropagation can train only a 2.7B LM with the same budget. We conduct comprehensive experiments across model types (masked and autoregressive LMs), model scales (up to 66B), and downstream tasks (classification, multiple-choice, and generation). Our results demonstrate that (1) MeZO significantly outperforms in-context learning and linear probing; (2) MeZO achieves comparable performance to fine-tuning with backpropagation across multiple tasks, with up to 12x memory reduction; (3) MeZO is compatible with both full-parameter and parameter-efficient tuning techniques such as LoRA and prefix tuning; (4) MeZO can effectively optimize non-differentiable objectives (e.g., maximizing accuracy or F1). We support our empirical findings with theoretical insights, highlighting how adequate pre-training and task prompts enable MeZO to fine-tune huge models, despite classical ZO analyses suggesting otherwise.

Smoothing the Landscape Boosts the Signal for SGD: Optimal Sample Complexity for Learning Single Index Models

We focus on the task of learning a single index model $\sigma(w^\star \cdot x)$ with respect to the isotropic Gaussian distribution in $d$ dimensions. Prior work has shown that the sample complexity of learning $w^\star$ is governed by the information exponent $k^\star$ of the link function $\sigma$, which is defined as the index of the first nonzero Hermite coefficient of $\sigma$. Ben Arous et al. (2021) showed that $n \gtrsim d^{k^\star-1}$ samples suffice for learning $w^\star$ and that this is tight for online SGD. However, the CSQ lower bound for gradient based methods only shows that $n \gtrsim d^{k^\star/2}$ samples are necessary. In this work, we close the gap between the upper and lower bounds by showing that online SGD on a smoothed loss learns $w^\star$ with $n \gtrsim d^{k^\star/2}$ samples. We also draw connections to statistical analyses of tensor PCA and to the implicit regularization effects of minibatch SGD on empirical losses.

Provable Guarantees for Nonlinear Feature Learning in Three-Layer Neural Networks

One of the central questions in the theory of deep learning is to understand how neural networks learn hierarchical features. The ability of deep networks to extract salient features is crucial to both their outstanding generalization ability and the modern deep learning paradigm of pretraining and finetuneing. However, this feature learning process remains poorly understood from a theoretical perspective, with existing analyses largely restricted to two-layer networks. In this work we show that three-layer neural networks have provably richer feature learning capabilities than two-layer networks. We analyze the features learned by a three-layer network trained with layer-wise gradient descent, and present a general purpose theorem which upper bounds the sample complexity and width needed to achieve low test error when the target has specific hierarchical structure. We instantiate our framework in specific statistical learning settings -- single-index models and functions of quadratic features -- and show that in the latter setting three-layer networks obtain a sample complexity improvement over all existing guarantees for two-layer networks. Crucially, this sample complexity improvement relies on the ability of three-layer networks to efficiently learn nonlinear features. We then establish a concrete optimization-based depth separation by constructing a function which is efficiently learnable via gradient descent on a three-layer network, yet cannot be learned efficiently by a two-layer network. Our work makes progress towards understanding the provable benefit of three-layer neural networks over two-layer networks in the feature learning regime.

Self-Stabilization: The Implicit Bias of Gradient Descent at the Edge of Stability

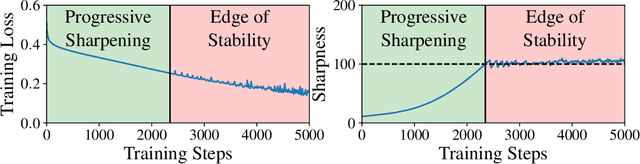
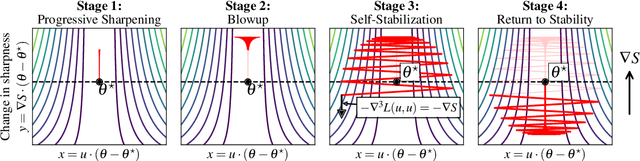
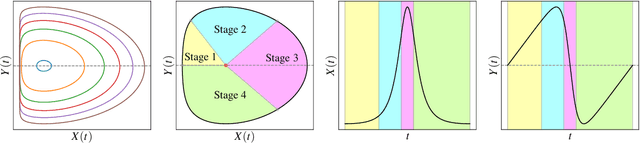
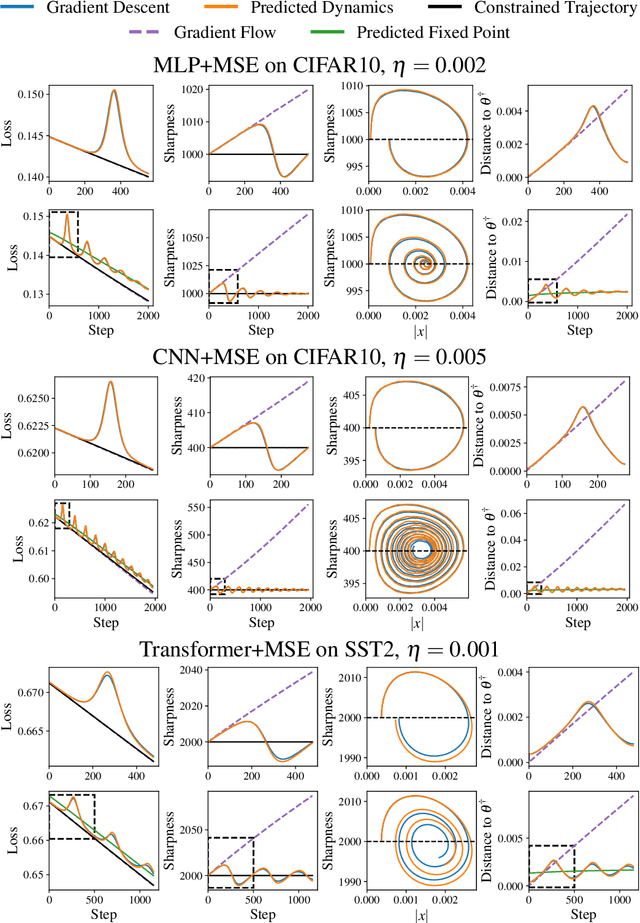
Traditional analyses of gradient descent show that when the largest eigenvalue of the Hessian, also known as the sharpness $S(\theta)$, is bounded by $2/\eta$, training is "stable" and the training loss decreases monotonically. Recent works, however, have observed that this assumption does not hold when training modern neural networks with full batch or large batch gradient descent. Most recently, Cohen et al. (2021) observed two important phenomena. The first, dubbed progressive sharpening, is that the sharpness steadily increases throughout training until it reaches the instability cutoff $2/\eta$. The second, dubbed edge of stability, is that the sharpness hovers at $2/\eta$ for the remainder of training while the loss continues decreasing, albeit non-monotonically. We demonstrate that, far from being chaotic, the dynamics of gradient descent at the edge of stability can be captured by a cubic Taylor expansion: as the iterates diverge in direction of the top eigenvector of the Hessian due to instability, the cubic term in the local Taylor expansion of the loss function causes the curvature to decrease until stability is restored. This property, which we call self-stabilization, is a general property of gradient descent and explains its behavior at the edge of stability. A key consequence of self-stabilization is that gradient descent at the edge of stability implicitly follows projected gradient descent (PGD) under the constraint $S(\theta) \le 2/\eta$. Our analysis provides precise predictions for the loss, sharpness, and deviation from the PGD trajectory throughout training, which we verify both empirically in a number of standard settings and theoretically under mild conditions. Our analysis uncovers the mechanism for gradient descent's implicit bias towards stability.

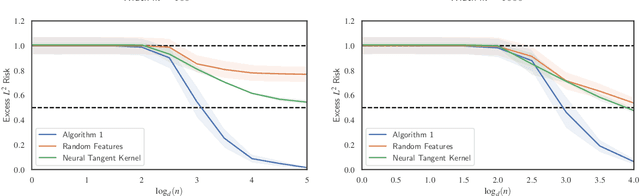
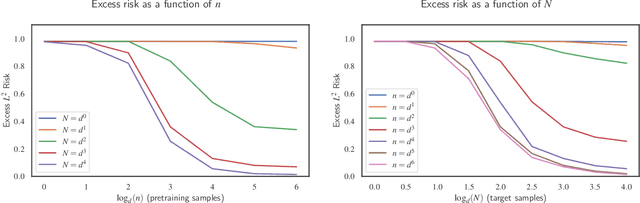
Neural Networks can Learn Representations with Gradient Descent

Significant theoretical work has established that in specific regimes, neural networks trained by gradient descent behave like kernel methods. However, in practice, it is known that neural networks strongly outperform their associated kernels. In this work, we explain this gap by demonstrating that there is a large class of functions which cannot be efficiently learned by kernel methods but can be easily learned with gradient descent on a two layer neural network outside the kernel regime by learning representations that are relevant to the target task. We also demonstrate that these representations allow for efficient transfer learning, which is impossible in the kernel regime. Specifically, we consider the problem of learning polynomials which depend on only a few relevant directions, i.e. of the form $f^\star(x) = g(Ux)$ where $U: \R^d \to \R^r$ with $d \gg r$. When the degree of $f^\star$ is $p$, it is known that $n \asymp d^p$ samples are necessary to learn $f^\star$ in the kernel regime. Our primary result is that gradient descent learns a representation of the data which depends only on the directions relevant to $f^\star$. This results in an improved sample complexity of $n\asymp d^2 r + dr^p$. Furthermore, in a transfer learning setup where the data distributions in the source and target domain share the same representation $U$ but have different polynomial heads we show that a popular heuristic for transfer learning has a target sample complexity independent of $d$.