Learning Compositional Functions with Transformers from Easy-to-Hard Data

Transformer-based language models have demonstrated impressive capabilities across a range of complex reasoning tasks. Prior theoretical work exploring the expressive power of transformers has shown that they can efficiently perform multi-step reasoning tasks involving parallelizable computations. However, the learnability of such constructions, particularly the conditions on the data distribution that enable efficient learning via gradient-based optimization, remains an open question. Towards answering this question, in this work we study the learnability of the $k$-fold composition task, which requires computing an interleaved composition of $k$ input permutations and $k$ hidden permutations, and can be expressed by a transformer with $O(\log k)$ layers. On the negative front, we prove a Statistical Query (SQ) lower bound showing that any SQ learner that makes only polynomially-many queries to an SQ oracle for the $k$-fold composition task distribution must have sample size exponential in $k$, thus establishing a statistical-computational gap. On the other hand, we show that this function class can be efficiently learned, with runtime and sample complexity polynomial in $k$, by gradient descent on an $O(\log k)$-depth transformer via two different curriculum learning strategies: one in which data consists of $k'$-fold composition functions with $k' \le k$ presented in increasing difficulty, and another in which all such data is presented simultaneously. Our work sheds light on the necessity and sufficiency of having both easy and hard examples in the data distribution for transformers to learn complex compositional tasks.

Emergence and scaling laws in SGD learning of shallow neural networks

We study the complexity of online stochastic gradient descent (SGD) for learning a two-layer neural network with $P$ neurons on isotropic Gaussian data: $f_*(\boldsymbol{x}) = \sum_{p=1}^P a_p\cdot \sigma(\langle\boldsymbol{x},\boldsymbol{v}_p^*\rangle)$, $\boldsymbol{x} \sim \mathcal{N}(0,\boldsymbol{I}_d)$, where the activation $\sigma:\mathbb{R}\to\mathbb{R}$ is an even function with information exponent $k_*>2$ (defined as the lowest degree in the Hermite expansion), $\{\boldsymbol{v}^*_p\}_{p\in[P]}\subset \mathbb{R}^d$ are orthonormal signal directions, and the non-negative second-layer coefficients satisfy $\sum_{p} a_p^2=1$. We focus on the challenging ``extensive-width'' regime $P\gg 1$ and permit diverging condition number in the second-layer, covering as a special case the power-law scaling $a_p\asymp p^{-\beta}$ where $\beta\in\mathbb{R}_{\ge 0}$. We provide a precise analysis of SGD dynamics for the training of a student two-layer network to minimize the mean squared error (MSE) objective, and explicitly identify sharp transition times to recover each signal direction. In the power-law setting, we characterize scaling law exponents for the MSE loss with respect to the number of training samples and SGD steps, as well as the number of parameters in the student neural network. Our analysis entails that while the learning of individual teacher neurons exhibits abrupt transitions, the juxtaposition of $P\gg 1$ emergent learning curves at different timescales leads to a smooth scaling law in the cumulative objective.

Understanding Factual Recall in Transformers via Associative Memories

Large language models have demonstrated an impressive ability to perform factual recall. Prior work has found that transformers trained on factual recall tasks can store information at a rate proportional to their parameter count. In our work, we show that shallow transformers can use a combination of associative memories to obtain such near optimal storage capacity. We begin by proving that the storage capacities of both linear and MLP associative memories scale linearly with parameter count. We next introduce a synthetic factual recall task, and prove that a transformer with a single layer of self-attention followed by an MLP can obtain 100% accuracy on the task whenever either the total number of self-attention parameters or MLP parameters scales (up to log factors) linearly with the number of facts. In particular, the transformer can trade off between using the value matrices or the MLP as an associative memory to store the dataset of facts. We complement these expressivity results with an analysis of the gradient flow trajectory of a simplified linear attention model trained on our factual recall task, where we show that the model exhibits sequential learning behavior.

Learning Hierarchical Polynomials of Multiple Nonlinear Features with Three-Layer Networks

In deep learning theory, a critical question is to understand how neural networks learn hierarchical features. In this work, we study the learning of hierarchical polynomials of \textit{multiple nonlinear features} using three-layer neural networks. We examine a broad class of functions of the form $f^{\star}=g^{\star}\circ \bp$, where $\bp:\mathbb{R}^{d} \rightarrow \mathbb{R}^{r}$ represents multiple quadratic features with $r \ll d$ and $g^{\star}:\mathbb{R}^{r}\rightarrow \mathbb{R}$ is a polynomial of degree $p$. This can be viewed as a nonlinear generalization of the multi-index model \citep{damian2022neural}, and also an expansion upon previous work that focused only on a single nonlinear feature, i.e. $r = 1$ \citep{nichani2023provable,wang2023learning}. Our primary contribution shows that a three-layer neural network trained via layerwise gradient descent suffices for \begin{itemize}\item complete recovery of the space spanned by the nonlinear features \item efficient learning of the target function $f^{\star}=g^{\star}\circ \bp$ or transfer learning of $f=g\circ \bp$ with a different link function \end{itemize} within $\widetilde{\cO}(d^4)$ samples and polynomial time. For such hierarchical targets, our result substantially improves the sample complexity ${\Theta}(d^{2p})$ of the kernel methods, demonstrating the power of efficient feature learning. It is important to highlight that{ our results leverage novel techniques and thus manage to go beyond all prior settings} such as single-index and multi-index models as well as models depending just on one nonlinear feature, contributing to a more comprehensive understanding of feature learning in deep learning.

How Transformers Learn Causal Structure with Gradient Descent

The incredible success of transformers on sequence modeling tasks can be largely attributed to the self-attention mechanism, which allows information to be transferred between different parts of a sequence. Self-attention allows transformers to encode causal structure which makes them particularly suitable for sequence modeling. However, the process by which transformers learn such causal structure via gradient-based training algorithms remains poorly understood. To better understand this process, we introduce an in-context learning task that requires learning latent causal structure. We prove that gradient descent on a simplified two-layer transformer learns to solve this task by encoding the latent causal graph in the first attention layer. The key insight of our proof is that the gradient of the attention matrix encodes the mutual information between tokens. As a consequence of the data processing inequality, the largest entries of this gradient correspond to edges in the latent causal graph. As a special case, when the sequences are generated from in-context Markov chains, we prove that transformers learn an induction head (Olsson et al., 2022). We confirm our theoretical findings by showing that transformers trained on our in-context learning task are able to recover a wide variety of causal structures.

Learning Hierarchical Polynomials with Three-Layer Neural Networks

We study the problem of learning hierarchical polynomials over the standard Gaussian distribution with three-layer neural networks. We specifically consider target functions of the form $h = g \circ p$ where $p : \mathbb{R}^d \rightarrow \mathbb{R}$ is a degree $k$ polynomial and $g: \mathbb{R} \rightarrow \mathbb{R}$ is a degree $q$ polynomial. This function class generalizes the single-index model, which corresponds to $k=1$, and is a natural class of functions possessing an underlying hierarchical structure. Our main result shows that for a large subclass of degree $k$ polynomials $p$, a three-layer neural network trained via layerwise gradient descent on the square loss learns the target $h$ up to vanishing test error in $\widetilde{\mathcal{O}}(d^k)$ samples and polynomial time. This is a strict improvement over kernel methods, which require $\widetilde \Theta(d^{kq})$ samples, as well as existing guarantees for two-layer networks, which require the target function to be low-rank. Our result also generalizes prior works on three-layer neural networks, which were restricted to the case of $p$ being a quadratic. When $p$ is indeed a quadratic, we achieve the information-theoretically optimal sample complexity $\widetilde{\mathcal{O}}(d^2)$, which is an improvement over prior work~\citep{nichani2023provable} requiring a sample size of $\widetilde\Theta(d^4)$. Our proof proceeds by showing that during the initial stage of training the network performs feature learning to recover the feature $p$ with $\widetilde{\mathcal{O}}(d^k)$ samples. This work demonstrates the ability of three-layer neural networks to learn complex features and as a result, learn a broad class of hierarchical functions.

Fine-Tuning Language Models with Just Forward Passes

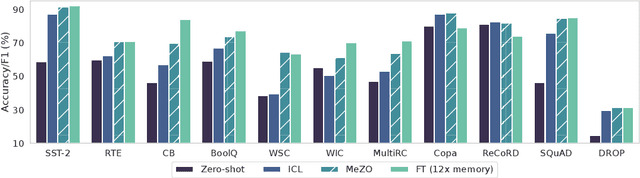
Fine-tuning language models (LMs) has yielded success on diverse downstream tasks, but as LMs grow in size, backpropagation requires a prohibitively large amount of memory. Zeroth-order (ZO) methods can in principle estimate gradients using only two forward passes but are theorized to be catastrophically slow for optimizing large models. In this work, we propose a memory-efficient zerothorder optimizer (MeZO), adapting the classical ZO-SGD method to operate in-place, thereby fine-tuning LMs with the same memory footprint as inference. For example, with a single A100 80GB GPU, MeZO can train a 30-billion parameter model, whereas fine-tuning with backpropagation can train only a 2.7B LM with the same budget. We conduct comprehensive experiments across model types (masked and autoregressive LMs), model scales (up to 66B), and downstream tasks (classification, multiple-choice, and generation). Our results demonstrate that (1) MeZO significantly outperforms in-context learning and linear probing; (2) MeZO achieves comparable performance to fine-tuning with backpropagation across multiple tasks, with up to 12x memory reduction; (3) MeZO is compatible with both full-parameter and parameter-efficient tuning techniques such as LoRA and prefix tuning; (4) MeZO can effectively optimize non-differentiable objectives (e.g., maximizing accuracy or F1). We support our empirical findings with theoretical insights, highlighting how adequate pre-training and task prompts enable MeZO to fine-tune huge models, despite classical ZO analyses suggesting otherwise.

Smoothing the Landscape Boosts the Signal for SGD: Optimal Sample Complexity for Learning Single Index Models

We focus on the task of learning a single index model $\sigma(w^\star \cdot x)$ with respect to the isotropic Gaussian distribution in $d$ dimensions. Prior work has shown that the sample complexity of learning $w^\star$ is governed by the information exponent $k^\star$ of the link function $\sigma$, which is defined as the index of the first nonzero Hermite coefficient of $\sigma$. Ben Arous et al. (2021) showed that $n \gtrsim d^{k^\star-1}$ samples suffice for learning $w^\star$ and that this is tight for online SGD. However, the CSQ lower bound for gradient based methods only shows that $n \gtrsim d^{k^\star/2}$ samples are necessary. In this work, we close the gap between the upper and lower bounds by showing that online SGD on a smoothed loss learns $w^\star$ with $n \gtrsim d^{k^\star/2}$ samples. We also draw connections to statistical analyses of tensor PCA and to the implicit regularization effects of minibatch SGD on empirical losses.

Provable Guarantees for Nonlinear Feature Learning in Three-Layer Neural Networks

One of the central questions in the theory of deep learning is to understand how neural networks learn hierarchical features. The ability of deep networks to extract salient features is crucial to both their outstanding generalization ability and the modern deep learning paradigm of pretraining and finetuneing. However, this feature learning process remains poorly understood from a theoretical perspective, with existing analyses largely restricted to two-layer networks. In this work we show that three-layer neural networks have provably richer feature learning capabilities than two-layer networks. We analyze the features learned by a three-layer network trained with layer-wise gradient descent, and present a general purpose theorem which upper bounds the sample complexity and width needed to achieve low test error when the target has specific hierarchical structure. We instantiate our framework in specific statistical learning settings -- single-index models and functions of quadratic features -- and show that in the latter setting three-layer networks obtain a sample complexity improvement over all existing guarantees for two-layer networks. Crucially, this sample complexity improvement relies on the ability of three-layer networks to efficiently learn nonlinear features. We then establish a concrete optimization-based depth separation by constructing a function which is efficiently learnable via gradient descent on a three-layer network, yet cannot be learned efficiently by a two-layer network. Our work makes progress towards understanding the provable benefit of three-layer neural networks over two-layer networks in the feature learning regime.

Self-Stabilization: The Implicit Bias of Gradient Descent at the Edge of Stability

Traditional analyses of gradient descent show that when the largest eigenvalue of the Hessian, also known as the sharpness $S(\theta)$, is bounded by $2/\eta$, training is "stable" and the training loss decreases monotonically. Recent works, however, have observed that this assumption does not hold when training modern neural networks with full batch or large batch gradient descent. Most recently, Cohen et al. (2021) observed two important phenomena. The first, dubbed progressive sharpening, is that the sharpness steadily increases throughout training until it reaches the instability cutoff $2/\eta$. The second, dubbed edge of stability, is that the sharpness hovers at $2/\eta$ for the remainder of training while the loss continues decreasing, albeit non-monotonically. We demonstrate that, far from being chaotic, the dynamics of gradient descent at the edge of stability can be captured by a cubic Taylor expansion: as the iterates diverge in direction of the top eigenvector of the Hessian due to instability, the cubic term in the local Taylor expansion of the loss function causes the curvature to decrease until stability is restored. This property, which we call self-stabilization, is a general property of gradient descent and explains its behavior at the edge of stability. A key consequence of self-stabilization is that gradient descent at the edge of stability implicitly follows projected gradient descent (PGD) under the constraint $S(\theta) \le 2/\eta$. Our analysis provides precise predictions for the loss, sharpness, and deviation from the PGD trajectory throughout training, which we verify both empirically in a number of standard settings and theoretically under mild conditions. Our analysis uncovers the mechanism for gradient descent's implicit bias towards stability.