Designing Composites with Target Effective Young's Modulus using Reinforcement Learning

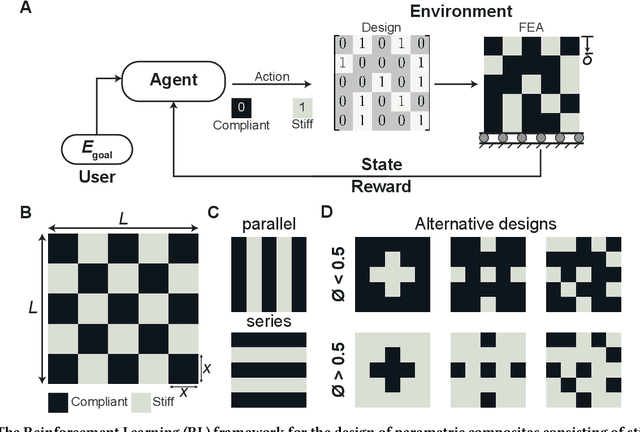
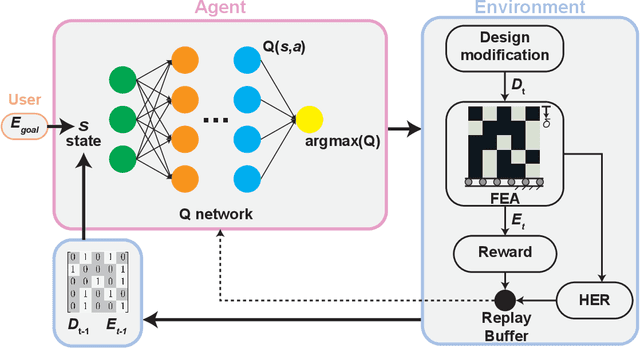
Advancements in additive manufacturing have enabled design and fabrication of materials and structures not previously realizable. In particular, the design space of composite materials and structures has vastly expanded, and the resulting size and complexity has challenged traditional design methodologies, such as brute force exploration and one factor at a time (OFAT) exploration, to find optimum or tailored designs. To address this challenge, supervised machine learning approaches have emerged to model the design space using curated training data; however, the selection of the training data is often determined by the user. In this work, we develop and utilize a Reinforcement learning (RL)-based framework for the design of composite structures which avoids the need for user-selected training data. For a 5 $\times$ 5 composite design space comprised of soft and compliant blocks of constituent material, we find that using this approach, the model can be trained using 2.78% of the total design space consists of $2^{25}$ design possibilities. Additionally, the developed RL-based framework is capable of finding designs at a success rate exceeding 90%. The success of this approach motivates future learning frameworks to utilize RL for the design of composites and other material systems.

Benchmarking the Performance of Bayesian Optimization across Multiple Experimental Materials Science Domains

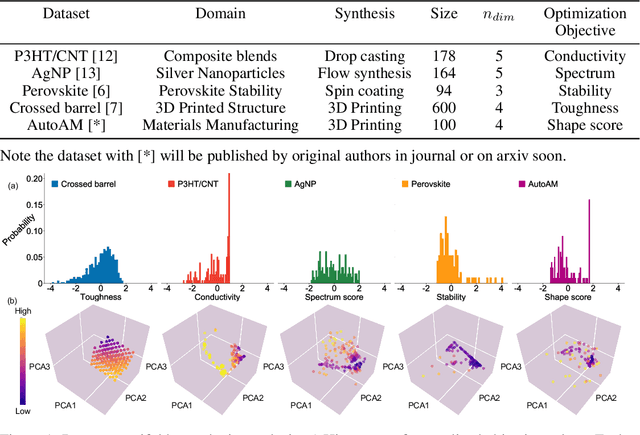
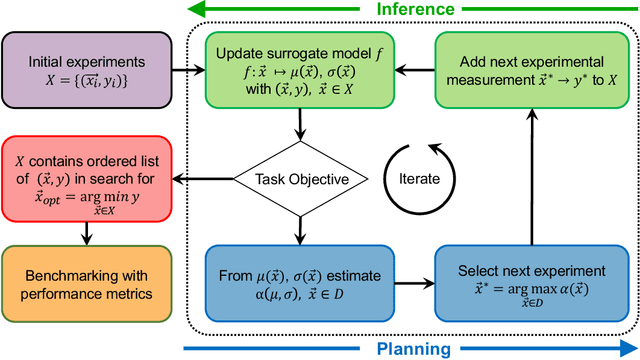
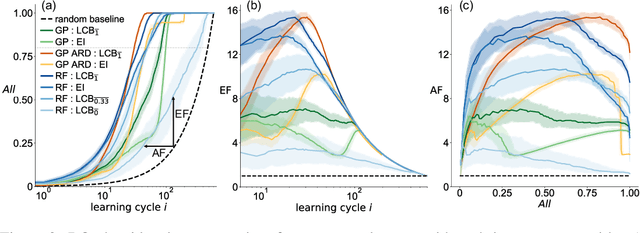
In the field of machine learning (ML) for materials optimization, active learning algorithms, such as Bayesian Optimization (BO), have been leveraged for guiding autonomous and high-throughput experimentation systems. However, very few studies have evaluated the efficiency of BO as a general optimization algorithm across a broad range of experimental materials science domains. In this work, we evaluate the performance of BO algorithms with a collection of surrogate model and acquisition function pairs across five diverse experimental materials systems, namely carbon nanotube polymer blends, silver nanoparticles, lead-halide perovskites, as well as additively manufactured polymer structures and shapes. By defining acceleration and enhancement metrics for general materials optimization objectives, we find that for surrogate model selection, Gaussian Process (GP) with anisotropic kernels (automatic relevance detection, ARD) and Random Forests (RF) have comparable performance and both outperform the commonly used GP without ARD. We discuss the implicit distributional assumptions of RF and GP, and the benefits of using GP with anisotropic kernels in detail. We provide practical insights for experimentalists on surrogate model selection of BO during materials optimization campaigns.