Benchmarking the Performance of Bayesian Optimization across Multiple Experimental Materials Science Domains

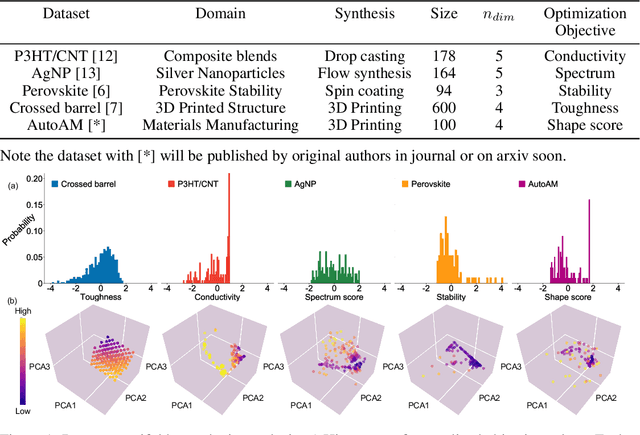
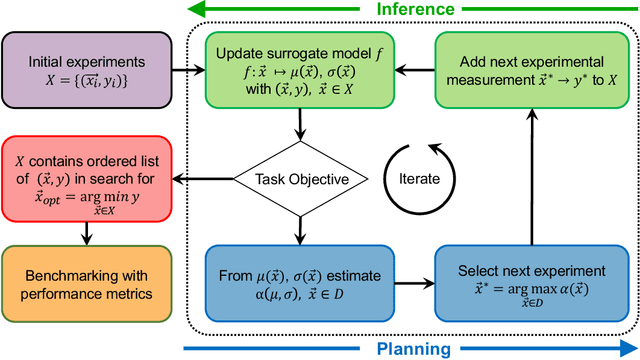
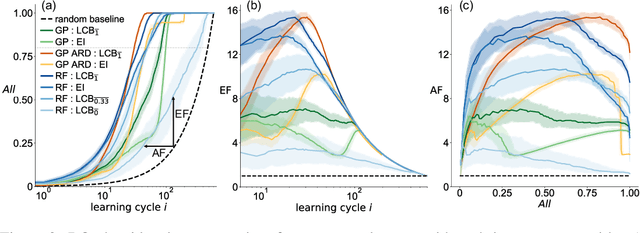
In the field of machine learning (ML) for materials optimization, active learning algorithms, such as Bayesian Optimization (BO), have been leveraged for guiding autonomous and high-throughput experimentation systems. However, very few studies have evaluated the efficiency of BO as a general optimization algorithm across a broad range of experimental materials science domains. In this work, we evaluate the performance of BO algorithms with a collection of surrogate model and acquisition function pairs across five diverse experimental materials systems, namely carbon nanotube polymer blends, silver nanoparticles, lead-halide perovskites, as well as additively manufactured polymer structures and shapes. By defining acceleration and enhancement metrics for general materials optimization objectives, we find that for surrogate model selection, Gaussian Process (GP) with anisotropic kernels (automatic relevance detection, ARD) and Random Forests (RF) have comparable performance and both outperform the commonly used GP without ARD. We discuss the implicit distributional assumptions of RF and GP, and the benefits of using GP with anisotropic kernels in detail. We provide practical insights for experimentalists on surrogate model selection of BO during materials optimization campaigns.

Inverse design of crystals using generalized invertible crystallographic representation

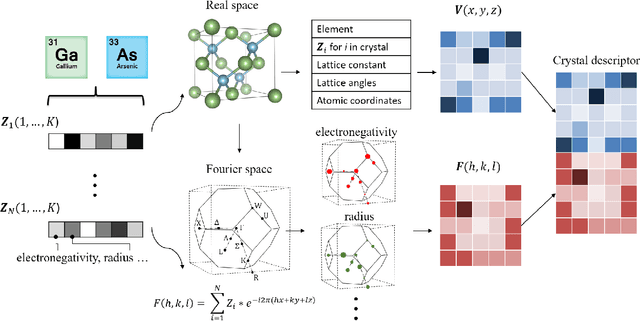
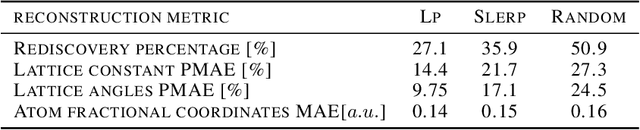
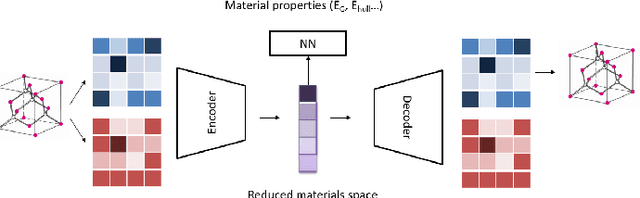
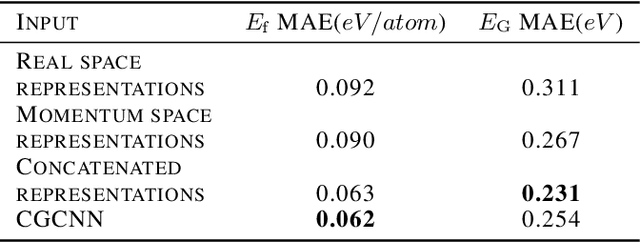
Deep learning has fostered many novel applications in materials informatics. However, the inverse design of inorganic crystals, $\textit{i.e.}$ generating new crystal structure with targeted properties, remains a grand challenge. An important ingredient for such generative models is an invertible representation that accesses the full periodic table. This is challenging due to limited data availability and the complexity of 3D periodic crystal structures. In this paper, we present a generalized invertible representation that encodes the crystallographic information into the descriptors in both real space and reciprocal space. Combining with a generative variational autoencoder (VAE), a wide range of crystallographic structures and chemistries with desired properties can be inverse-designed. We show that our VAE model predicts novel crystal structures that do not exist in the training and test database (Materials Project) with targeted formation energies and band gaps. We validate those predicted crystals by first-principles calculations. Finally, to design solids with practical applications, we address the sparse label problem by building a semi-supervised VAE and demonstrate its successful prediction of unique thermoelectric materials