Investigating self-supervised features for expressive, multilingual voice conversion

Voice conversion (VC) systems are widely used for several applications, from speaker anonymisation to personalised speech synthesis. Supervised approaches learn a mapping between different speakers using parallel data, which is expensive to produce. Unsupervised approaches are typically trained to reconstruct the input signal, which is composed of the content and the speaker information. Disentangling these components is a challenge and often leads to speaker leakage or prosodic information removal. In this paper, we explore voice conversion by leveraging the potential of self-supervised learning (SSL). A combination of the latent representations of SSL models, concatenated with speaker embeddings, is fed to a vocoder which is trained to reconstruct the input. Zero-shot voice conversion results show that this approach allows to keep the prosody and content of the source speaker while matching the speaker similarity of a VC system based on phonetic posteriorgrams (PPGs).

Lightweight End-to-end Text-to-speech Synthesis for low resource on-device applications

Recent works have shown that modelling raw waveform directly from text in an end-to-end (E2E) fashion produces more natural-sounding speech than traditional neural text-to-speech (TTS) systems based on a cascade or two-stage approach. However, current E2E state-of-the-art models are computationally complex and memory-consuming, making them unsuitable for real-time offline on-device applications in low-resource scenarios. To address this issue, we propose a Lightweight E2E-TTS (LE2E) model that generates high-quality speech requiring minimal computational resources. We evaluate the proposed model on the LJSpeech dataset and show that it achieves state-of-the-art performance while being up to $90\%$ smaller in terms of model parameters and $10\times$ faster in real-time-factor. Furthermore, we demonstrate that the proposed E2E training paradigm achieves better quality compared to an equivalent architecture trained in a two-stage approach. Our results suggest that LE2E is a promising approach for developing real-time, high quality, low-resource TTS applications for on-device applications.

Voice Filter: Few-shot text-to-speech speaker adaptation using voice conversion as a post-processing module

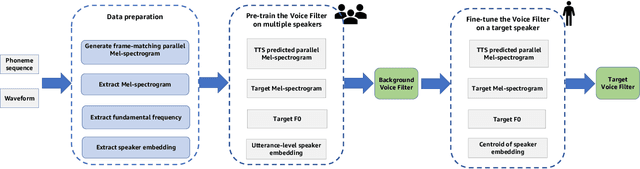
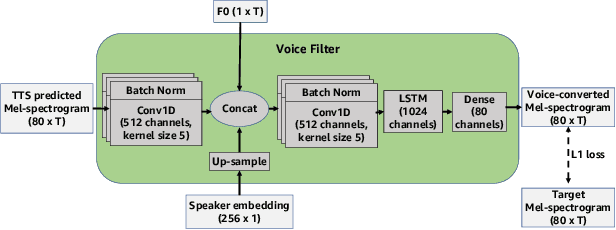
State-of-the-art text-to-speech (TTS) systems require several hours of recorded speech data to generate high-quality synthetic speech. When using reduced amounts of training data, standard TTS models suffer from speech quality and intelligibility degradations, making training low-resource TTS systems problematic. In this paper, we propose a novel extremely low-resource TTS method called Voice Filter that uses as little as one minute of speech from a target speaker. It uses voice conversion (VC) as a post-processing module appended to a pre-existing high-quality TTS system and marks a conceptual shift in the existing TTS paradigm, framing the few-shot TTS problem as a VC task. Furthermore, we propose to use a duration-controllable TTS system to create a parallel speech corpus to facilitate the VC task. Results show that the Voice Filter outperforms state-of-the-art few-shot speech synthesis techniques in terms of objective and subjective metrics on one minute of speech on a diverse set of voices, while being competitive against a TTS model built on 30 times more data.

Improving the expressiveness of neural vocoding with non-affine Normalizing Flows

This paper proposes a general enhancement to the Normalizing Flows (NF) used in neural vocoding. As a case study, we improve expressive speech vocoding with a revamped Parallel Wavenet (PW). Specifically, we propose to extend the affine transformation of PW to the more expressive invertible non-affine function. The greater expressiveness of the improved PW leads to better-perceived signal quality and naturalness in the waveform reconstruction and text-to-speech (TTS) tasks. We evaluate the model across different speaking styles on a multi-speaker, multi-lingual dataset. In the waveform reconstruction task, the proposed model closes the naturalness and signal quality gap from the original PW to recordings by $10\%$, and from other state-of-the-art neural vocoding systems by more than $60\%$. We also demonstrate improvements in objective metrics on the evaluation test set with L2 Spectral Distance and Cross-Entropy reduced by $3\%$ and $6\unicode{x2030}$ comparing to the affine PW. Furthermore, we extend the probability density distillation procedure proposed by the original PW paper, so that it works with any non-affine invertible and differentiable function.