Neural Stochastic Flows: Solver-Free Modelling and Inference for SDE Solutions

Stochastic differential equations (SDEs) are well suited to modelling noisy and irregularly sampled time series found in finance, physics, and machine learning. Traditional approaches require costly numerical solvers to sample between arbitrary time points. We introduce Neural Stochastic Flows (NSFs) and their latent variants, which directly learn (latent) SDE transition laws using conditional normalising flows with architectural constraints that preserve properties inherited from stochastic flows. This enables one-shot sampling between arbitrary states and yields up to two orders of magnitude speed-ups at large time gaps. Experiments on synthetic SDE simulations and on real-world tracking and video data show that NSFs maintain distributional accuracy comparable to numerical approaches while dramatically reducing computation for arbitrary time-point sampling.

Adaptive Heterogeneous Mixtures of Normalising Flows for Robust Variational Inference

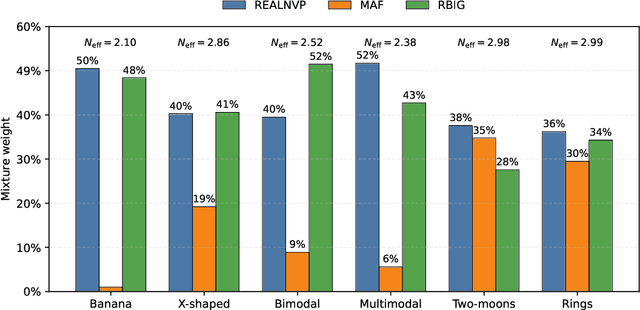
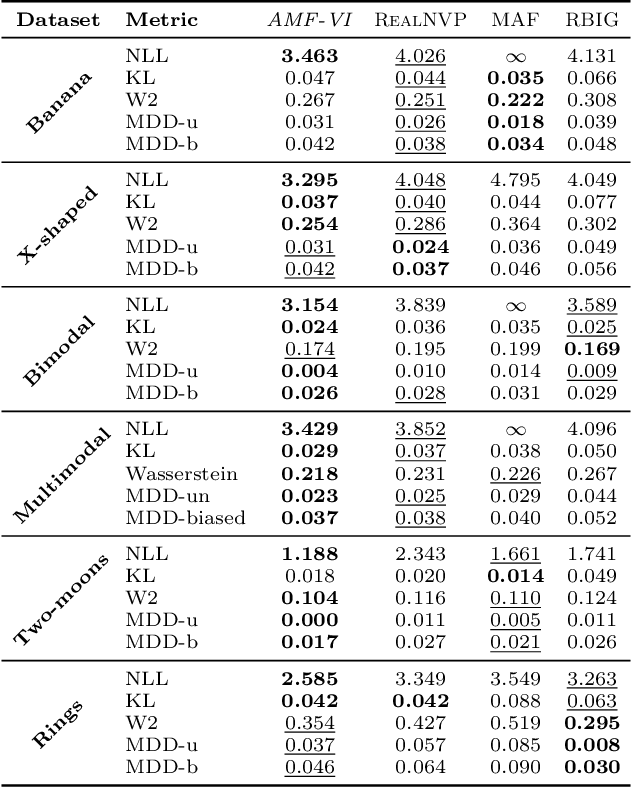
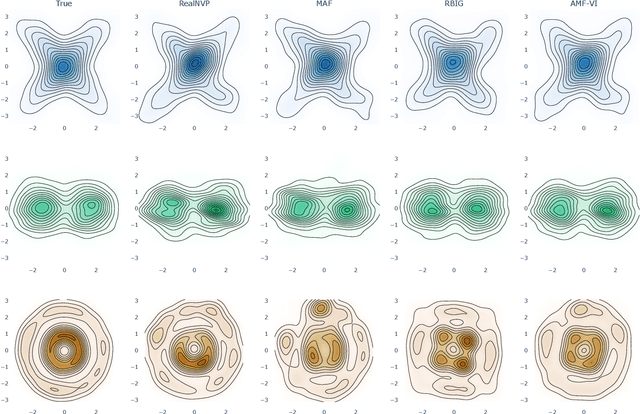
Normalising-flow variational inference (VI) can approximate complex posteriors, yet single-flow models often behave inconsistently across qualitatively different distributions. We propose Adaptive Mixture Flow Variational Inference (AMF-VI), a heterogeneous mixture of complementary flows (MAF, RealNVP, RBIG) trained in two stages: (i) sequential expert training of individual flows, and (ii) adaptive global weight estimation via likelihood-driven updates, without per-sample gating or architectural changes. Evaluated on six canonical posterior families of banana, X-shape, two-moons, rings, a bimodal, and a five-mode mixture, AMF-VI achieves consistently lower negative log-likelihood than each single-flow baseline and delivers stable gains in transport metrics (Wasserstein-2) and maximum mean discrepancy (MDD), indicating improved robustness across shapes and modalities. The procedure is efficient and architecture-agnostic, incurring minimal overhead relative to standard flow training, and demonstrates that adaptive mixtures of diverse flows provide a reliable route to robust VI across diverse posterior families whilst preserving each expert's inductive bias.

Learning Satellite Attitude Dynamics with Physics-Informed Normalising Flow

Attitude control is a fundamental aspect of spacecraft operations. Model Predictive Control (MPC) has emerged as a powerful strategy for these tasks, relying on accurate models of the system dynamics to optimize control actions over a prediction horizon. In scenarios where physics models are incomplete, difficult to derive, or computationally expensive, machine learning offers a flexible alternative by learning the system behavior directly from data. However, purely data-driven models often struggle with generalization and stability, especially when applied to inputs outside their training domain. To address these limitations, we investigate the benefits of incorporating Physics-Informed Neural Networks (PINNs) into the learning of spacecraft attitude dynamics, comparing their performance with that of purely data-driven approaches. Using a Real-valued Non-Volume Preserving (Real NVP) neural network architecture with a self-attention mechanism, we trained several models on simulated data generated with the Basilisk simulator. Two training strategies were considered: a purely data-driven baseline and a physics-informed variant to improve robustness and stability. Our results demonstrate that the inclusion of physics-based information significantly enhances the performance in terms of the mean relative error of the best architectures found by 27.08%. These advantages are particularly evident when the learned models are integrated into an MPC framework, where PINN-based models consistently outperform their purely data-driven counterparts in terms of control accuracy and robustness, yielding improvements of up to 42.86% in performance stability error and increased robustness-to-noise.

Improved Ground State Estimation in Quantum Field Theories via Normalising Flow-Assisted Neural Quantum States

We propose a hybrid variational framework that enhances Neural Quantum States (NQS) with a Normalising Flow-based sampler to improve the expressivity and trainability of quantum many-body wavefunctions. Our approach decouples the sampling task from the variational ansatz by learning a continuous flow model that targets a discretised, amplitude-supported subspace of the Hilbert space. This overcomes limitations of Markov Chain Monte Carlo (MCMC) and autoregressive methods, especially in regimes with long-range correlations and volume-law entanglement. Applied to the transverse-field Ising model with both short- and long-range interactions, our method achieves comparable ground state energy errors with state-of-the-art matrix product states and lower energies than autoregressive NQS. For systems up to 50 spins, we demonstrate high accuracy and robust convergence across a wide range of coupling strengths, including regimes where competing methods fail. Our results showcase the utility of flow-assisted sampling as a scalable tool for quantum simulation and offer a new approach toward learning expressive quantum states in high-dimensional Hilbert spaces.

JAPAN: Joint Adaptive Prediction Areas with Normalising-Flows

Conformal prediction provides a model-agnostic framework for uncertainty quantification with finite-sample validity guarantees, making it an attractive tool for constructing reliable prediction sets. However, existing approaches commonly rely on residual-based conformity scores, which impose geometric constraints and struggle when the underlying distribution is multimodal. In particular, they tend to produce overly conservative prediction areas centred around the mean, often failing to capture the true shape of complex predictive distributions. In this work, we introduce JAPAN (Joint Adaptive Prediction Areas with Normalising-Flows), a conformal prediction framework that uses density-based conformity scores. By leveraging flow-based models, JAPAN estimates the (predictive) density and constructs prediction areas by thresholding on the estimated density scores, enabling compact, potentially disjoint, and context-adaptive regions that retain finite-sample coverage guarantees. We theoretically motivate the efficiency of JAPAN and empirically validate it across multivariate regression and forecasting tasks, demonstrating good calibration and tighter prediction areas compared to existing baselines. We also provide several \emph{extensions} adding flexibility to our proposed framework.

CFMI: Flow Matching for Missing Data Imputation

We introduce conditional flow matching for imputation (CFMI), a new general-purpose method to impute missing data. The method combines continuous normalising flows, flow-matching, and shared conditional modelling to deal with intractabilities of traditional multiple imputation. Our comparison with nine classical and state-of-the-art imputation methods on 24 small to moderate-dimensional tabular data sets shows that CFMI matches or outperforms both traditional and modern techniques across a wide range of metrics. Applying the method to zero-shot imputation of time-series data, we find that it matches the accuracy of a related diffusion-based method while outperforming it in terms of computational efficiency. Overall, CFMI performs at least as well as traditional methods on lower-dimensional data while remaining scalable to high-dimensional settings, matching or exceeding the performance of other deep learning-based approaches, making it a go-to imputation method for a wide range of data types and dimensionalities.

Fault injection analysis of Real NVP normalising flow model for satellite anomaly detection

Satellites are used for a multitude of applications, including communications, Earth observation, and space science. Neural networks and deep learning-based approaches now represent the state-of-the-art to enhance the performance and efficiency of these tasks. Given that satellites are susceptible to various faults, one critical application of Artificial Intelligence (AI) is fault detection. However, despite the advantages of neural networks, these systems are vulnerable to radiation errors, which can significantly impact their reliability. Ensuring the dependability of these solutions requires extensive testing and validation, particularly using fault injection methods. This study analyses a physics-informed (PI) real-valued non-volume preserving (Real NVP) normalizing flow model for fault detection in space systems, with a focus on resilience to Single-Event Upsets (SEUs). We present a customized fault injection framework in TensorFlow to assess neural network resilience. Fault injections are applied through two primary methods: Layer State injection, targeting internal network components such as weights and biases, and Layer Output injection, which modifies layer outputs across various activations. Fault types include zeros, random values, and bit-flip operations, applied at varying levels and across different network layers. Our findings reveal several critical insights, such as the significance of bit-flip errors in critical bits, that can lead to substantial performance degradation or even system failure. With this work, we aim to exhaustively study the resilience of Real NVP models against errors due to radiation, providing a means to guide the implementation of fault tolerance measures.

Savage-Dickey density ratio estimation with normalizing flows for Bayesian model comparison

A core motivation of science is to evaluate which scientific model best explains observed data. Bayesian model comparison provides a principled statistical approach to comparing scientific models and has found widespread application within cosmology and astrophysics. Calculating the Bayesian evidence is computationally challenging, especially as we continue to explore increasingly more complex models. The Savage-Dickey density ratio (SDDR) provides a method to calculate the Bayes factor (evidence ratio) between two nested models using only posterior samples from the super model. The SDDR requires the calculation of a normalised marginal distribution over the extra parameters of the super model, which has typically been performed using classical density estimators, such as histograms. Classical density estimators, however, can struggle to scale to high-dimensional settings. We introduce a neural SDDR approach using normalizing flows that can scale to settings where the super model contains a large number of extra parameters. We demonstrate the effectiveness of this neural SDDR methodology applied to both toy and realistic cosmological examples. For a field-level inference setting, we show that Bayes factors computed for a Bayesian hierarchical model (BHM) and simulation-based inference (SBI) approach are consistent, providing further validation that SBI extracts as much cosmological information from the field as the BHM approach. The SDDR estimator with normalizing flows is implemented in the open-source harmonic Python package.

Communicating Likelihoods with Normalising Flows

We present a machine-learning-based workflow to model an unbinned likelihood from its samples. A key advancement over existing approaches is the validation of the learned likelihood using rigorous statistical tests of the joint distribution, such as the Kolmogorov-Smirnov test of the joint distribution. Our method enables the reliable communication of experimental and phenomenological likelihoods for subsequent analyses. We demonstrate its effectiveness through three case studies in high-energy physics. To support broader adoption, we provide an open-source reference implementation, nabu.

Conformalised Conditional Normalising Flows for Joint Prediction Regions in time series

Conformal Prediction offers a powerful framework for quantifying uncertainty in machine learning models, enabling the construction of prediction sets with finite-sample validity guarantees. While easily adaptable to non-probabilistic models, applying conformal prediction to probabilistic generative models, such as Normalising Flows is not straightforward. This work proposes a novel method to conformalise conditional normalising flows, specifically addressing the problem of obtaining prediction regions for multi-step time series forecasting. Our approach leverages the flexibility of normalising flows to generate potentially disjoint prediction regions, leading to improved predictive efficiency in the presence of potential multimodal predictive distributions.