Nonlinearity as Rank: Generative Low-Rank Adapter with Radial Basis Functions

Low-rank adaptation (LoRA) approximates the update of a pretrained weight matrix using the product of two low-rank matrices. However, standard LoRA follows an explicit-rank paradigm, where increasing model capacity requires adding more rows or columns (i.e., basis vectors) to the low-rank matrices, leading to substantial parameter growth. In this paper, we find that these basis vectors exhibit significant parameter redundancy and can be compactly represented by lightweight nonlinear functions. Therefore, we propose Generative Low-Rank Adapter (GenLoRA), which replaces explicit basis vector storage with nonlinear basis vector generation. Specifically, GenLoRA maintains a latent vector for each low-rank matrix and employs a set of lightweight radial basis functions (RBFs) to synthesize the basis vectors. Each RBF requires far fewer parameters than an explicit basis vector, enabling higher parameter efficiency in GenLoRA. Extensive experiments across multiple datasets and architectures show that GenLoRA attains higher effective LoRA ranks under smaller parameter budgets, resulting in superior fine-tuning performance. The code is available at https://anonymous.4open.science/r/GenLoRA-1519.

Mixed-Precision Embeddings for Large-Scale Recommendation Models

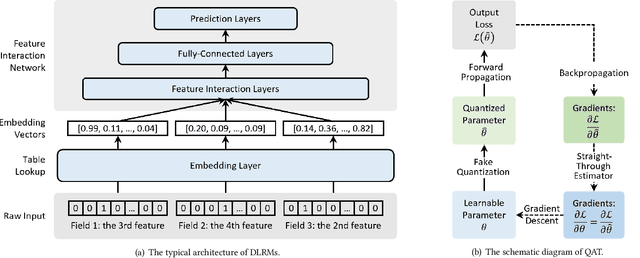
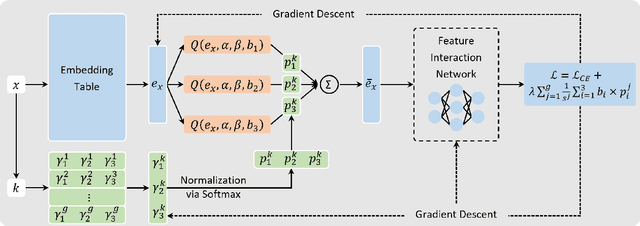
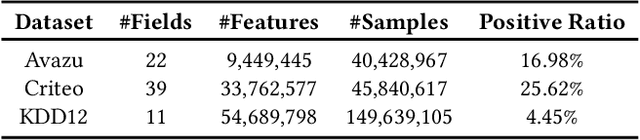
Embedding techniques have become essential components of large databases in the deep learning era. By encoding discrete entities, such as words, items, or graph nodes, into continuous vector spaces, embeddings facilitate more efficient storage, retrieval, and processing in large databases. Especially in the domain of recommender systems, millions of categorical features are encoded as unique embedding vectors, which facilitates the modeling of similarities and interactions among features. However, numerous embedding vectors can result in significant storage overhead. In this paper, we aim to compress the embedding table through quantization techniques. Given that features vary in importance levels, we seek to identify an appropriate precision for each feature to balance model accuracy and memory usage. To this end, we propose a novel embedding compression method, termed Mixed-Precision Embeddings (MPE). Specifically, to reduce the size of the search space, we first group features by frequency and then search precision for each feature group. MPE further learns the probability distribution over precision levels for each feature group, which can be used to identify the most suitable precision with a specially designed sampling strategy. Extensive experiments on three public datasets demonstrate that MPE significantly outperforms existing embedding compression methods. Remarkably, MPE achieves about 200x compression on the Criteo dataset without comprising the prediction accuracy.