General Methods for Evaluating Collision Probability of Different Types of Theta-phi Positioners

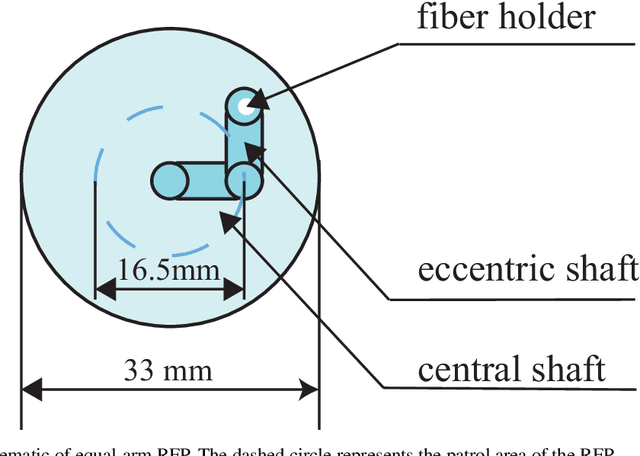
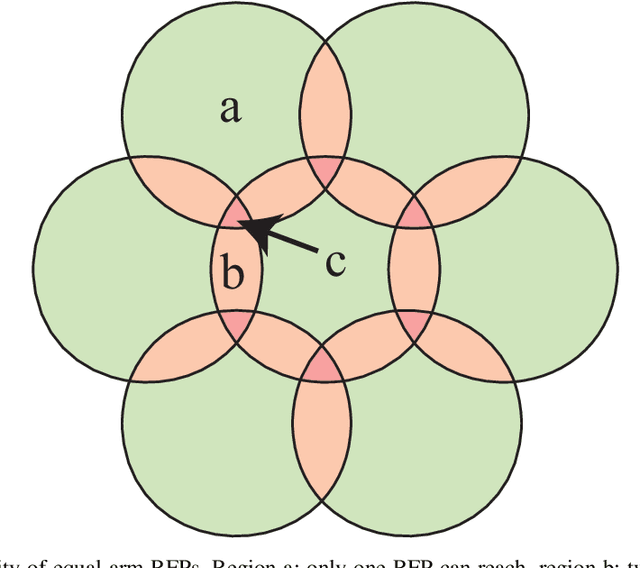
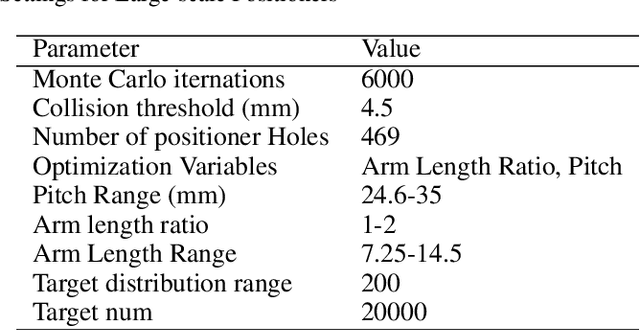
In many modern astronomical facilities, multi-object telescopes are crucial instruments. Most of these telescopes have thousands of robotic fiber positioners(RFPs) installed on their focal plane, sharing an overlapping workspace. Collisions between RFPs during their movement can result in some targets becoming unreachable and cause structural damage. Therefore, it is necessary to reasonably assess and evaluate the collision probability of the RFPs. In this study, we propose a mathematical models of collision probability and validate its results using Monte Carlo simulations. In addition, a new collision calculation method is proposed for faster calculation(nearly 0.15% of original time). Simulation experiments have verified that our method can evaluate the collision probability between RFPs with both equal and unequal arm lengths. Additionally, we found that adopting a target distribution based on a Poisson distribution can reduce the collision probability by approximately 2.6% on average.

A Constraints Fusion-induced Symmetric Nonnegative Matrix Factorization Approach for Community Detection

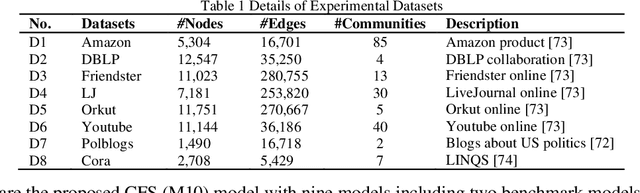
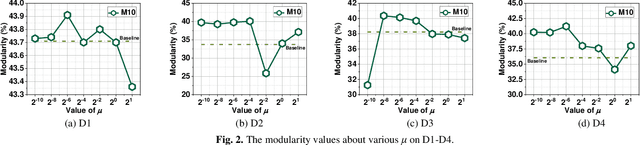
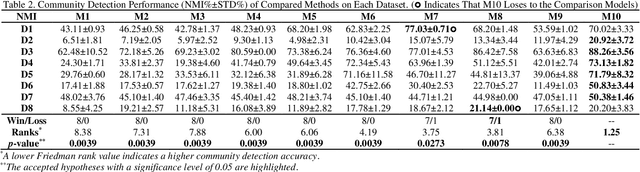
Community is a fundamental and critical characteristic of an undirected social network, making community detection be a vital yet thorny issue in network representation learning. A symmetric and non-negative matrix factorization (SNMF) model is frequently adopted to address this issue owing to its great interpretability and scalability. However, it adopts a single latent factor matrix to represent an undirected network for precisely representing its symmetry, which leads to loss of representation learning ability due to the reduced latent space. Motivated by this discovery, this paper proposes a novel Constraints Fusion-induced Symmetric Nonnegative Matrix Factorization (CFS) model that adopts three-fold ideas: a) Representing a target undirected network with multiple latent factor matrices, thus preserving its representation learning capacity; b) Incorporating a symmetry-regularizer that preserves the symmetry of the learnt low-rank approximation to the adjacency matrix into the loss function, thus making the resultant detector well-aware of the target network's symmetry; and c) Introducing a graph-regularizer that preserves local invariance of the network's intrinsic geometry, thus making the achieved detector well-aware of community structure within the target network. Extensively empirical studies on eight real-world social networks from industrial applications demonstrate that the proposed CFS model significantly outperforms state-of-the-art models in achieving highly-accurate community detection results.

High-order Order Proximity-Incorporated, Symmetry and Graph-Regularized Nonnegative Matrix Factorization for Community Detection

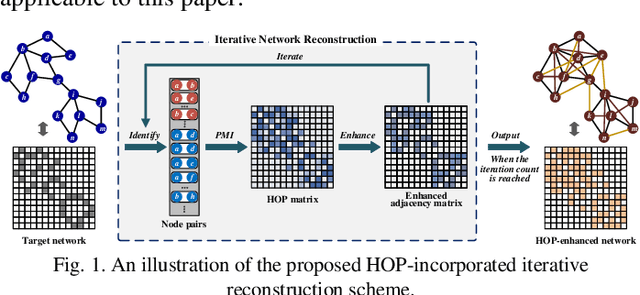
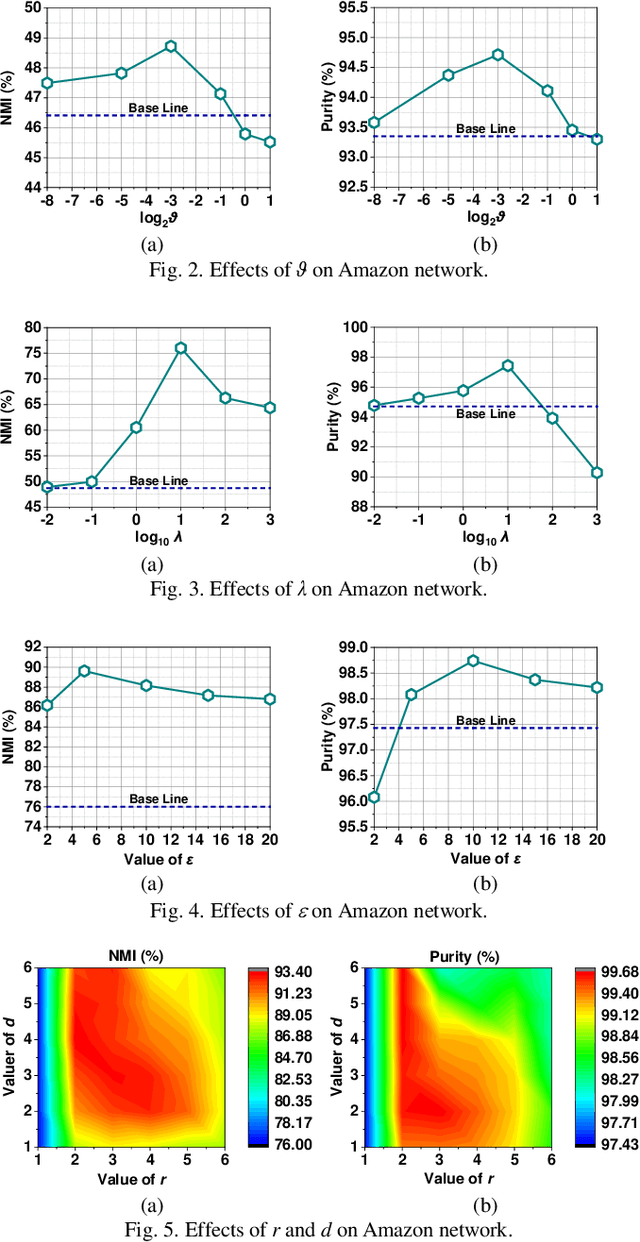
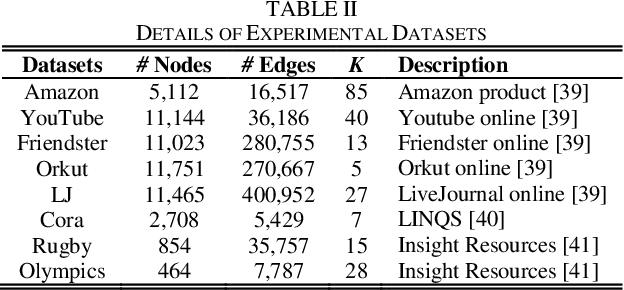
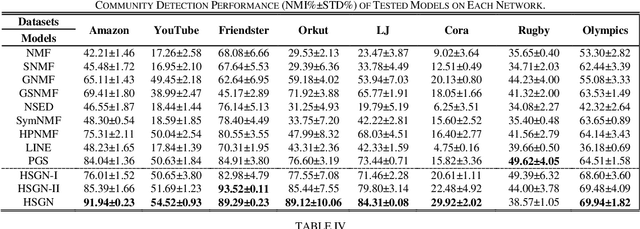
Community describes the functional mechanism of a network, making community detection serve as a fundamental graph tool for various real applications like discovery of social circle. To date, a Symmetric and Non-negative Matrix Factorization (SNMF) model has been frequently adopted to address this issue owing to its high interpretability and scalability. However, most existing SNMF-based community detection methods neglect the high-order connection patterns in a network. Motivated by this discovery, in this paper, we propose a High-Order Proximity (HOP)-incorporated, Symmetry and Graph-regularized NMF (HSGN) model that adopts the following three-fold ideas: a) adopting a weighted pointwise mutual information (PMI)-based approach to measure the HOP indices among nodes in a network; b) leveraging an iterative reconstruction scheme to encode the captured HOP into the network; and c) introducing a symmetry and graph-regularized NMF algorithm to detect communities accurately. Extensive empirical studies on eight real-world networks demonstrate that an HSGN-based community detector significantly outperforms both benchmark and state-of-the-art community detectors in providing highly-accurate community detection results.

Doping: A technique for efficient compression of LSTM models using sparse structured additive matrices

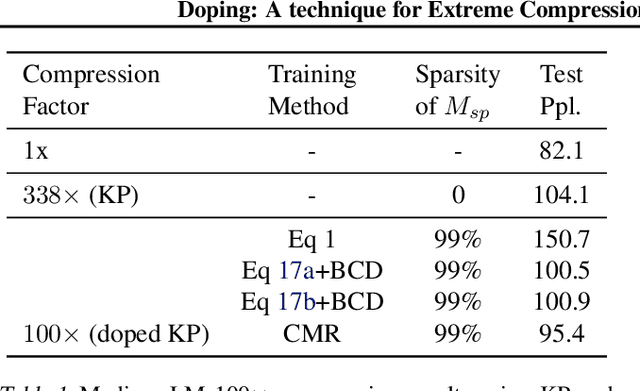
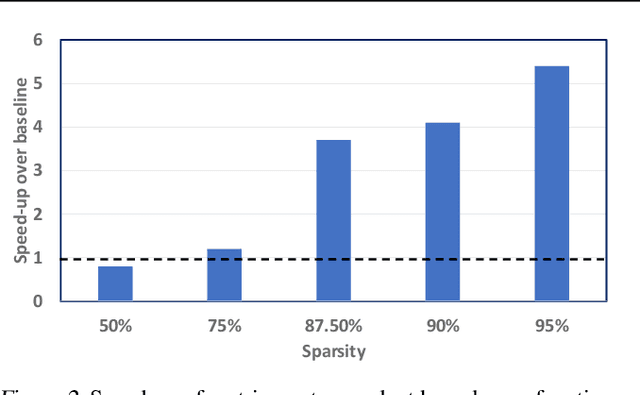
Structured matrices, such as those derived from Kronecker products (KP), are effective at compressing neural networks, but can lead to unacceptable accuracy loss when applied to large models. In this paper, we propose the notion of doping -- addition of an extremely sparse matrix to a structured matrix. Doping facilitates additional degrees of freedom for a small number of parameters, allowing them to independently diverge from the fixed structure. To train LSTMs with doped structured matrices, we introduce the additional parameter matrix while slowly annealing its sparsity level. However, we find that performance degrades as we slowly sparsify the doping matrix, due to co-matrix adaptation (CMA) between the structured and the sparse matrices. We address this over dependence on the sparse matrix using a co-matrix dropout regularization (CMR) scheme. We provide empirical evidence to show that doping, CMA and CMR are concepts generally applicable to multiple structured matrices (Kronecker Product, LMF, Hybrid Matrix Decomposition). Additionally, results with doped kronecker product matrices demonstrate state-of-the-art accuracy at large compression factors (10 - 25x) across 4 natural language processing applications with minor loss in accuracy. Doped KP compression technique outperforms previous state-of-the art compression results by achieving 1.3 - 2.4x higher compression factor at a similar accuracy, while also beating strong alternatives like pruning and low-rank methods by a large margin (8% or more). Additionally, we show that doped KP can be deployed on commodity hardware using the current software stack and achieve 2.5 - 5.5x inference run-time speed-up over baseline.