High-order Order Proximity-Incorporated, Symmetry and Graph-Regularized Nonnegative Matrix Factorization for Community Detection
Paper and Code
Mar 08, 2022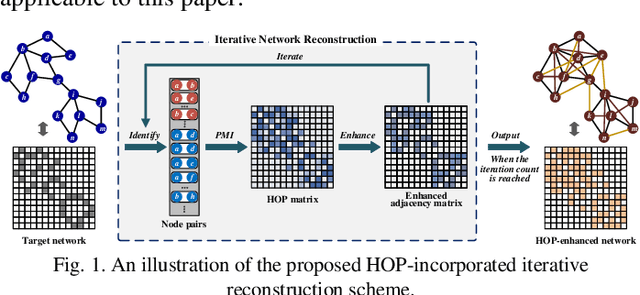
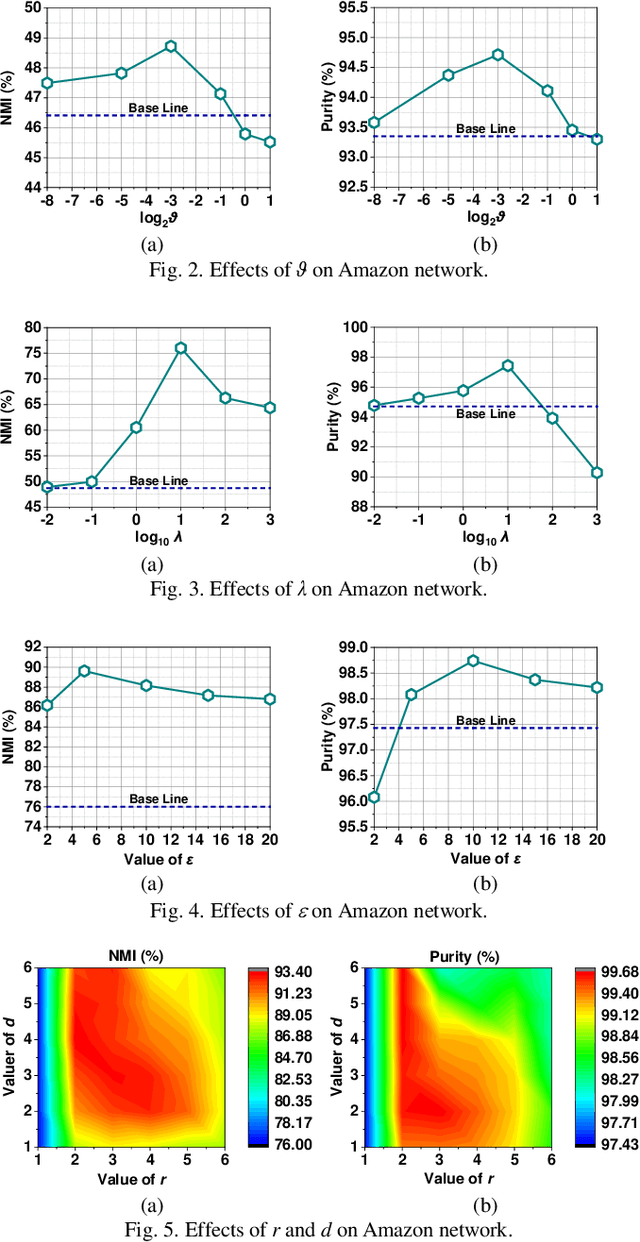
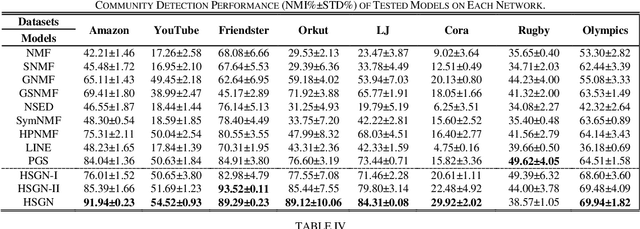
Community describes the functional mechanism of a network, making community detection serve as a fundamental graph tool for various real applications like discovery of social circle. To date, a Symmetric and Non-negative Matrix Factorization (SNMF) model has been frequently adopted to address this issue owing to its high interpretability and scalability. However, most existing SNMF-based community detection methods neglect the high-order connection patterns in a network. Motivated by this discovery, in this paper, we propose a High-Order Proximity (HOP)-incorporated, Symmetry and Graph-regularized NMF (HSGN) model that adopts the following three-fold ideas: a) adopting a weighted pointwise mutual information (PMI)-based approach to measure the HOP indices among nodes in a network; b) leveraging an iterative reconstruction scheme to encode the captured HOP into the network; and c) introducing a symmetry and graph-regularized NMF algorithm to detect communities accurately. Extensive empirical studies on eight real-world networks demonstrate that an HSGN-based community detector significantly outperforms both benchmark and state-of-the-art community detectors in providing highly-accurate community detection results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge