Towards Reliable Time Series Forecasting under Future Uncertainty: Ambiguity and Novelty Rejection Mechanisms

In real-world time series forecasting, uncertainty and lack of reliable evaluation pose significant challenges. Notably, forecasting errors often arise from underfitting in-distribution data and failing to handle out-of-distribution inputs. To enhance model reliability, we introduce a dual rejection mechanism combining ambiguity and novelty rejection. Ambiguity rejection, using prediction error variance, allows the model to abstain under low confidence, assessed through historical error variance analysis without future ground truth. Novelty rejection, employing Variational Autoencoders and Mahalanobis distance, detects deviations from training data. This dual approach improves forecasting reliability in dynamic environments by reducing errors and adapting to data changes, advancing reliability in complex scenarios.

TimeSieve: Extracting Temporal Dynamics through Information Bottlenecks

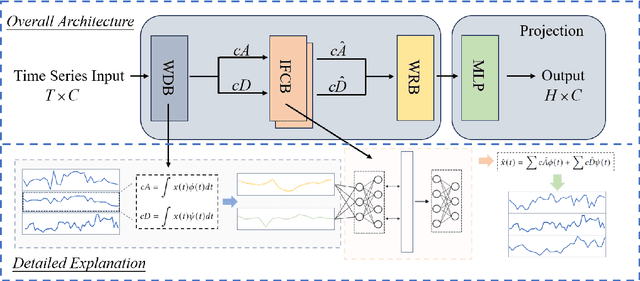
Time series forecasting has become an increasingly popular research area due to its critical applications in various real-world domains such as traffic management, weather prediction, and financial analysis. Despite significant advancements, existing models face notable challenges, including the necessity of manual hyperparameter tuning for different datasets, and difficulty in effectively distinguishing signal from redundant features in data characterized by strong seasonality. These issues hinder the generalization and practical application of time series forecasting models. To solve this issues, we propose an innovative time series forecasting model TimeSieve designed to address these challenges. Our approach employs wavelet transforms to preprocess time series data, effectively capturing multi-scale features without the need for additional parameters or manual hyperparameter tuning. Additionally, we introduce the information bottleneck theory that filters out redundant features from both detail and approximation coefficients, retaining only the most predictive information. This combination reduces significantly improves the model's accuracy. Extensive experiments demonstrate that our model outperforms existing state-of-the-art methods on 70\% of the datasets, achieving higher predictive accuracy and better generalization across diverse datasets. Our results validate the effectiveness of our approach in addressing the key challenges in time series forecasting, paving the way for more reliable and efficient predictive models in practical applications. The code for our model is available at https://github.com/xll0328/TimeSieve.

Learning-based Control for PMSM Using Distributed Gaussian Processes with Optimal Aggregation Strategy

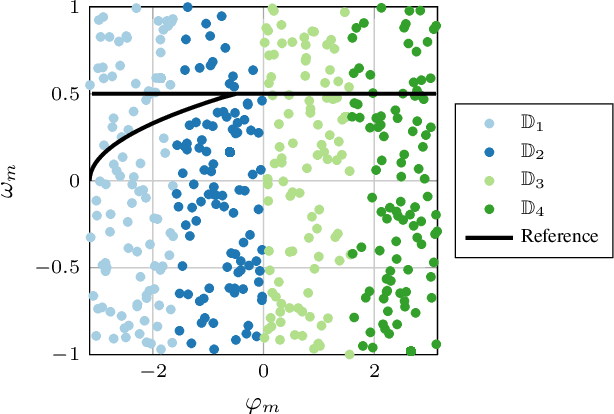
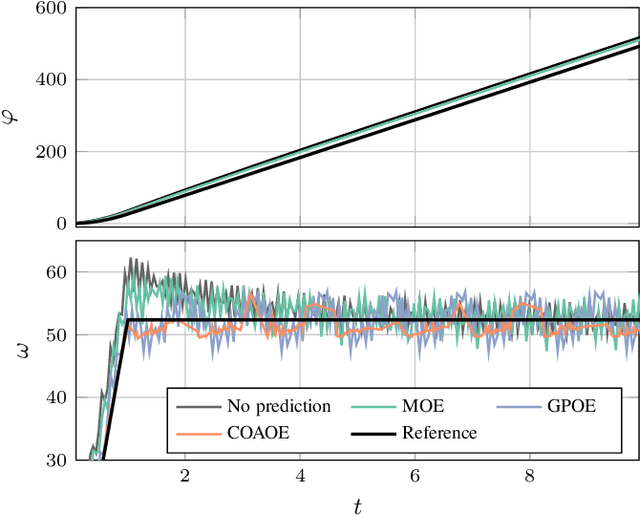
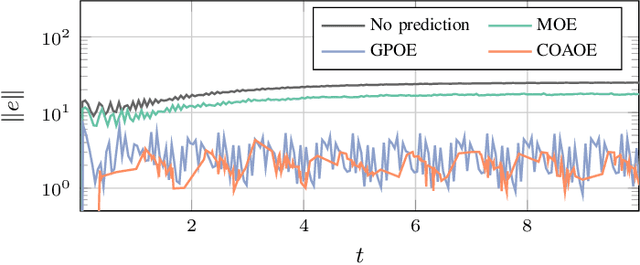
The growing demand for accurate control in varying and unknown environments has sparked a corresponding increase in the requirements for power supply components, including permanent magnet synchronous motors (PMSMs). To infer the unknown part of the system, machine learning techniques are widely employed, especially Gaussian process regression (GPR) due to its flexibility of continuous system modeling and its guaranteed performance. For practical implementation, distributed GPR is adopted to alleviate the high computational complexity. However, the study of distributed GPR from a control perspective remains an open problem. In this paper, a control-aware optimal aggregation strategy of distributed GPR for PMSMs is proposed based on the Lyapunov stability theory. This strategy exclusively leverages the posterior mean, thereby obviating the need for computationally intensive calculations associated with posterior variance in alternative approaches. Moreover, the straightforward calculation process of our proposed strategy lends itself to seamless implementation in high-frequency PMSM control. The effectiveness of the proposed strategy is demonstrated in the simulations.