Unsupervised Learning of Structured Representations via Closed-Loop Transcription

This paper proposes an unsupervised method for learning a unified representation that serves both discriminative and generative purposes. While most existing unsupervised learning approaches focus on a representation for only one of these two goals, we show that a unified representation can enjoy the mutual benefits of having both. Such a representation is attainable by generalizing the recently proposed \textit{closed-loop transcription} framework, known as CTRL, to the unsupervised setting. This entails solving a constrained maximin game over a rate reduction objective that expands features of all samples while compressing features of augmentations of each sample. Through this process, we see discriminative low-dimensional structures emerge in the resulting representations. Under comparable experimental conditions and network complexities, we demonstrate that these structured representations enable classification performance close to state-of-the-art unsupervised discriminative representations, and conditionally generated image quality significantly higher than that of state-of-the-art unsupervised generative models. Source code can be found at https://github.com/Delay-Xili/uCTRL.

Intra-Instance VICReg: Bag of Self-Supervised Image Patch Embedding

Recently, self-supervised learning (SSL) has achieved tremendous empirical advancements in learning image representation. However, our understanding and knowledge of the representation are still limited. This work shows that the success of the SOTA siamese-network-based SSL approaches is primarily based on learning a representation of image patches. Particularly, we show that when we learn a representation only for fixed-scale image patches and aggregate different patch representations linearly for an image (instance), it can achieve on par or even better results than the baseline methods on several benchmarks. Further, we show that the patch representation aggregation can also improve various SOTA baseline methods by a large margin. We also establish a formal connection between the SSL objective and the image patches co-occurrence statistics modeling, which supplements the prevailing invariance perspective. By visualizing the nearest neighbors of different image patches in the embedding space and projection space, we show that while the projection has more invariance, the embedding space tends to preserve more equivariance and locality. Finally, we propose a hypothesis for the future direction based on the discovery of this work.

Neural Manifold Clustering and Embedding

Given a union of non-linear manifolds, non-linear subspace clustering or manifold clustering aims to cluster data points based on manifold structures and also learn to parameterize each manifold as a linear subspace in a feature space. Deep neural networks have the potential to achieve this goal under highly non-linear settings given their large capacity and flexibility. We argue that achieving manifold clustering with neural networks requires two essential ingredients: a domain-specific constraint that ensures the identification of the manifolds, and a learning algorithm for embedding each manifold to a linear subspace in the feature space. This work shows that many constraints can be implemented by data augmentation. For subspace feature learning, Maximum Coding Rate Reduction (MCR$^2$) objective can be used. Putting them together yields {\em Neural Manifold Clustering and Embedding} (NMCE), a novel method for general purpose manifold clustering, which significantly outperforms autoencoder-based deep subspace clustering. Further, on more challenging natural image datasets, NMCE can also outperform other algorithms specifically designed for clustering. Qualitatively, we demonstrate that NMCE learns a meaningful and interpretable feature space. As the formulation of NMCE is closely related to several important Self-supervised learning (SSL) methods, we believe this work can help us build a deeper understanding on SSL representation learning.

A Neural Network MCMC sampler that maximizes Proposal Entropy

Markov Chain Monte Carlo (MCMC) methods sample from unnormalized probability distributions and offer guarantees of exact sampling. However, in the continuous case, unfavorable geometry of the target distribution can greatly limit the efficiency of MCMC methods. Augmenting samplers with neural networks can potentially improve their efficiency. Previous neural network based samplers were trained with objectives that either did not explicitly encourage exploration, or used a L2 jump objective which could only be applied to well structured distributions. Thus it seems promising to instead maximize the proposal entropy for adapting the proposal to distributions of any shape. To allow direct optimization of the proposal entropy, we propose a neural network MCMC sampler that has a flexible and tractable proposal distribution. Specifically, our network architecture utilizes the gradient of the target distribution for generating proposals. Our model achieves significantly higher efficiency than previous neural network MCMC techniques in a variety of sampling tasks. Further, the sampler is applied on training of a convergent energy-based model of natural images. The adaptive sampler achieves unbiased sampling with significantly higher proposal entropy than Langevin dynamics sampler.

Complex Amplitude-Phase Boltzmann Machines

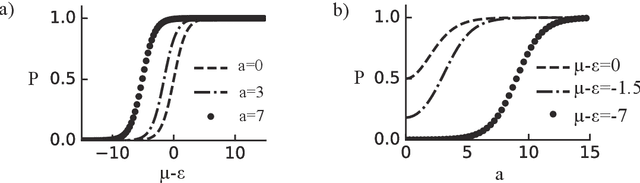
We extend the framework of Boltzmann machines to a network of complex-valued neurons with variable amplitudes, referred to as Complex Amplitude-Phase Boltzmann machine (CAP-BM). The model is capable of performing unsupervised learning on the amplitude and relative phase distribution in complex data. The sampling rule of the Gibbs distribution and the learning rules of the model are presented. Learning in a Complex Amplitude-Phase restricted Boltzmann machine (CAP-RBM) is demonstrated on synthetic complex-valued images, and handwritten MNIST digits transformed by a complex wavelet transform. Specifically, we show the necessity of a new amplitude-amplitude coupling term in our model. The proposed model is potentially valuable for machine learning tasks involving complex-valued data with amplitude variation, and for developing algorithms for novel computation hardware, such as coupled oscillators and neuromorphic hardware, on which Boltzmann sampling can be executed in the complex domain.

Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces

Energy-Based Models (EBMs) outputs unmormalized log-probability values given data samples. Such an estimation is essential in a variety of applications such as sample generation, denoising, sample restoration, outlier detection, Bayesian reasoning, and many more. However, standard maximum likelihood training is computationally expensive due to the requirement of sampling the model distribution. Score matching potentially alleviates this problem, and denoising score matching is a particularly convenient version. However, previous works do not produce models capable of high quality sample synthesis in high dimensional datasets from random initialization. We believe that is because the score is only matched over a single noise scale, which corresponds to a small set in high-dimensional space. To overcome this limitation, here we instead learn an energy function using denoising score matching over all noise scales. When sampled from random initialization using Annealed Langevin Dynamics and single-step denoising jump, our model produced high-quality samples comparable to state-of-the-art techniques such as GANs. The learned model also provide density information and set a new sample quality baseline in energy-based models. We further demonstrate that the proposed method generalizes well with an image inpainting task.