DA-MoE: Addressing Depth-Sensitivity in Graph-Level Analysis through Mixture of Experts

Graph neural networks (GNNs) are gaining popularity for processing graph-structured data. In real-world scenarios, graph data within the same dataset can vary significantly in scale. This variability leads to depth-sensitivity, where the optimal depth of GNN layers depends on the scale of the graph data. Empirically, fewer layers are sufficient for message passing in smaller graphs, while larger graphs typically require deeper networks to capture long-range dependencies and global features. However, existing methods generally use a fixed number of GNN layers to generate representations for all graphs, overlooking the depth-sensitivity issue in graph structure data. To address this challenge, we propose the depth adaptive mixture of expert (DA-MoE) method, which incorporates two main improvements to GNN backbone: \textbf{1)} DA-MoE employs different GNN layers, each considered an expert with its own parameters. Such a design allows the model to flexibly aggregate information at different scales, effectively addressing the depth-sensitivity issue in graph data. \textbf{2)} DA-MoE utilizes GNN to capture the structural information instead of the linear projections in the gating network. Thus, the gating network enables the model to capture complex patterns and dependencies within the data. By leveraging these improvements, each expert in DA-MoE specifically learns distinct graph patterns at different scales. Furthermore, comprehensive experiments on the TU dataset and open graph benchmark (OGB) have shown that DA-MoE consistently surpasses existing baselines on various tasks, including graph, node, and link-level analyses. The code are available at \url{https://github.com/Celin-Yao/DA-MoE}.

Dual-perspective Cross Contrastive Learning in Graph Transformers

Graph contrastive learning (GCL) is a popular method for leaning graph representations by maximizing the consistency of features across augmented views. Traditional GCL methods utilize single-perspective i.e. data or model-perspective) augmentation to generate positive samples, restraining the diversity of positive samples. In addition, these positive samples may be unreliable due to uncontrollable augmentation strategies that potentially alter the semantic information. To address these challenges, this paper proposed a innovative framework termed dual-perspective cross graph contrastive learning (DC-GCL), which incorporates three modifications designed to enhance positive sample diversity and reliability: 1) We propose dual-perspective augmentation strategy that provide the model with more diverse training data, enabling the model effective learning of feature consistency across different views. 2) From the data perspective, we slightly perturb the original graphs using controllable data augmentation, effectively preserving their semantic information. 3) From the model perspective, we enhance the encoder by utilizing more powerful graph transformers instead of graph neural networks. Based on the model's architecture, we propose three pruning-based strategies to slightly perturb the encoder, providing more reliable positive samples. These modifications collectively form the DC-GCL's foundation and provide more diverse and reliable training inputs, offering significant improvements over traditional GCL methods. Extensive experiments on various benchmarks demonstrate that DC-GCL consistently outperforms different baselines on various datasets and tasks.

Hi-GMAE: Hierarchical Graph Masked Autoencoders

Graph Masked Autoencoders (GMAEs) have emerged as a notable self-supervised learning approach for graph-structured data. Existing GMAE models primarily focus on reconstructing node-level information, categorizing them as single-scale GMAEs. This methodology, while effective in certain contexts, tends to overlook the complex hierarchical structures inherent in many real-world graphs. For instance, molecular graphs exhibit a clear hierarchical organization in the form of the atoms-functional groups-molecules structure. Hence, the inability of single-scale GMAE models to incorporate these hierarchical relationships often leads to their inadequate capture of crucial high-level graph information, resulting in a noticeable decline in performance. To address this limitation, we propose Hierarchical Graph Masked AutoEncoders (Hi-GMAE), a novel multi-scale GMAE framework designed to handle the hierarchical structures within graphs. First, Hi-GMAE constructs a multi-scale graph hierarchy through graph pooling, enabling the exploration of graph structures across different granularity levels. To ensure masking uniformity of subgraphs across these scales, we propose a novel coarse-to-fine strategy that initiates masking at the coarsest scale and progressively back-projects the mask to the finer scales. Furthermore, we integrate a gradual recovery strategy with the masking process to mitigate the learning challenges posed by completely masked subgraphs. Diverging from the standard graph neural network (GNN) used in GMAE models, Hi-GMAE modifies its encoder and decoder into hierarchical structures. This entails using GNN at the finer scales for detailed local graph analysis and employing a graph transformer at coarser scales to capture global information. Our experiments on 15 graph datasets consistently demonstrate that Hi-GMAE outperforms 17 state-of-the-art self-supervised competitors.

Gradformer: Graph Transformer with Exponential Decay

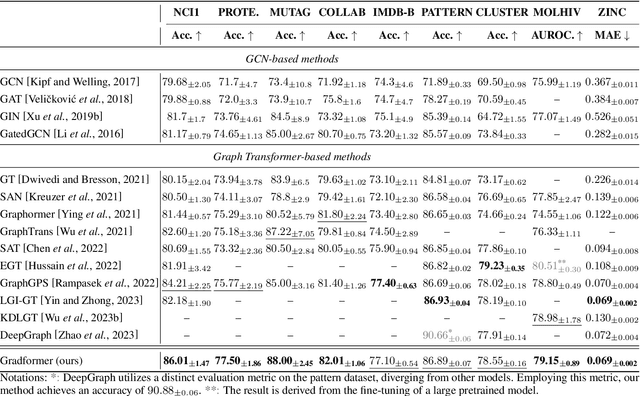
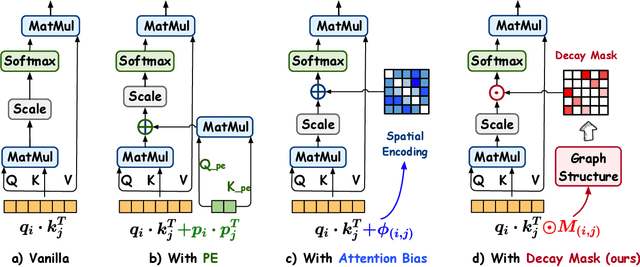
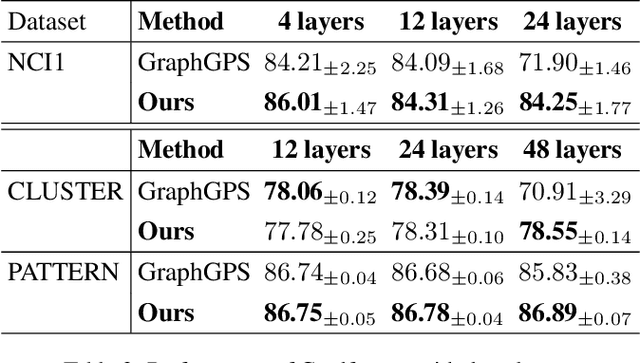
Graph Transformers (GTs) have demonstrated their advantages across a wide range of tasks. However, the self-attention mechanism in GTs overlooks the graph's inductive biases, particularly biases related to structure, which are crucial for the graph tasks. Although some methods utilize positional encoding and attention bias to model inductive biases, their effectiveness is still suboptimal analytically. Therefore, this paper presents Gradformer, a method innovatively integrating GT with the intrinsic inductive bias by applying an exponential decay mask to the attention matrix. Specifically, the values in the decay mask matrix diminish exponentially, correlating with the decreasing node proximities within the graph structure. This design enables Gradformer to retain its ability to capture information from distant nodes while focusing on the graph's local details. Furthermore, Gradformer introduces a learnable constraint into the decay mask, allowing different attention heads to learn distinct decay masks. Such an design diversifies the attention heads, enabling a more effective assimilation of diverse structural information within the graph. Extensive experiments on various benchmarks demonstrate that Gradformer consistently outperforms the Graph Neural Network and GT baseline models in various graph classification and regression tasks. Additionally, Gradformer has proven to be an effective method for training deep GT models, maintaining or even enhancing accuracy compared to shallow models as the network deepens, in contrast to the significant accuracy drop observed in other GT models.Codes are available at \url{https://github.com/LiuChuang0059/Gradformer}.