Exploring explicit coarse-grained structure in artificial neural networks

We propose to employ the hierarchical coarse-grained structure in the artificial neural networks explicitly to improve the interpretability without degrading performance. The idea has been applied in two situations. One is a neural network called TaylorNet, which aims to approximate the general mapping from input data to output result in terms of Taylor series directly, without resorting to any magic nonlinear activations. The other is a new setup for data distillation, which can perform multi-level abstraction of the input dataset and generate new data that possesses the relevant features of the original dataset and can be used as references for classification. In both cases, the coarse-grained structure plays an important role in simplifying the network and improving both the interpretability and efficiency. The validity has been demonstrated on MNIST and CIFAR-10 datasets. Further improvement and some open questions related are also discussed.

Enabling Lightweight Fine-tuning for Pre-trained Language Model Compression based on Matrix Product Operators

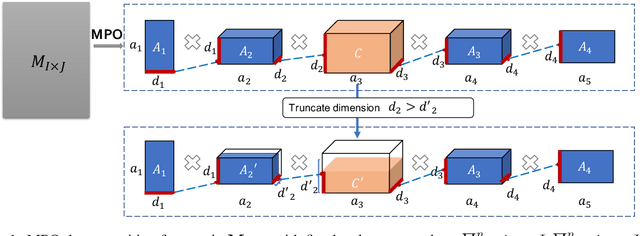
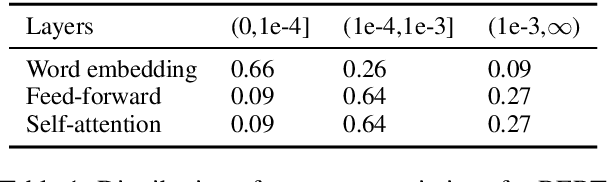
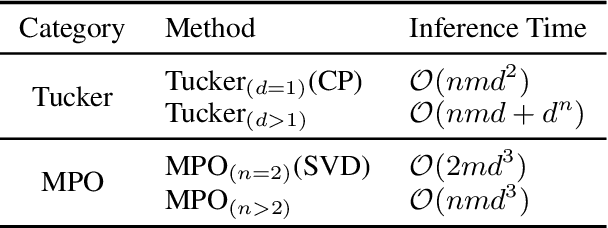
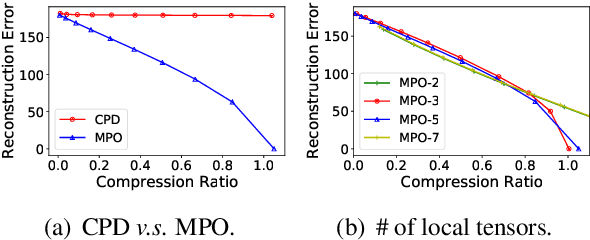
This paper presents a novel pre-trained language models (PLM) compression approach based on the matrix product operator (short as MPO) from quantum many-body physics. It can decompose an original matrix into central tensors (containing the core information) and auxiliary tensors (with only a small proportion of parameters). With the decomposed MPO structure, we propose a novel fine-tuning strategy by only updating the parameters from the auxiliary tensors, and design an optimization algorithm for MPO-based approximation over stacked network architectures. Our approach can be applied to the original or the compressed PLMs in a general way, which derives a lighter network and significantly reduces the parameters to be fine-tuned. Extensive experiments have demonstrated the effectiveness of the proposed approach in model compression, especially the reduction in finetuning parameters (91% reduction on average).

Compressing deep neural networks by matrix product operators

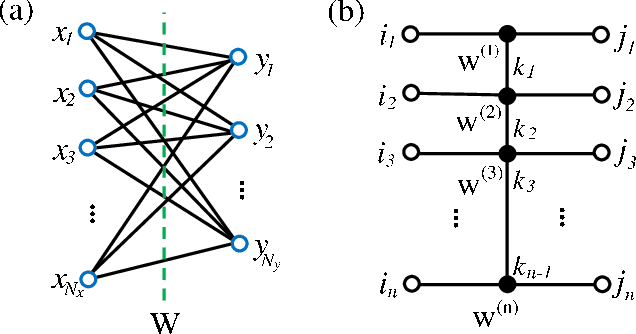
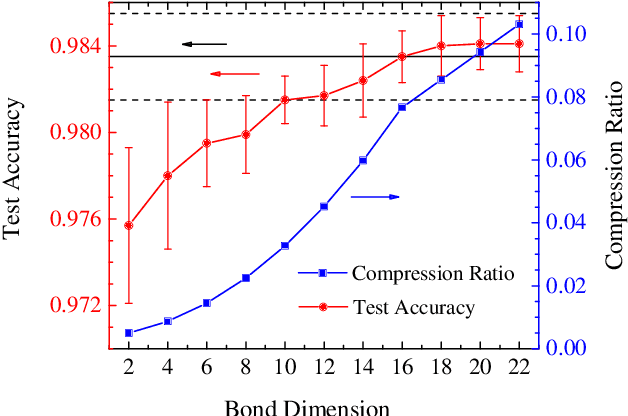
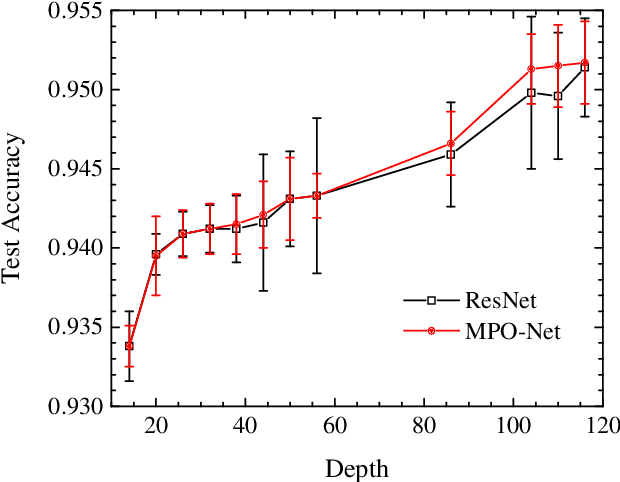
A deep neural network is a parameterization of a multi-layer mapping of signals in terms of many alternatively arranged linear and nonlinear transformations. The linear transformations, which are generally used in the fully-connected as well as convolutional layers, contain most of the variational parameters that are trained and stored. Compressing a deep neural network to reduce its number of variational parameters but not its prediction power is an important but challenging problem towards the establishment of an optimized scheme in training efficiently these parameters and in lowering the risk of overfitting. Here we show that this problem can be effectively solved by representing linear transformations with matrix product operators (MPO). We have tested this approach in five main neural networks, including FC2, LeNet-5, VGG, ResNet, and DenseNet on two widely used datasets, namely MNIST and CIFAR-10, and found that this MPO representation indeed sets up a faithful and efficient mapping between input and output signals, which can keep or even improve the prediction accuracy with dramatically reduced number of parameters.