Generalized Lanczos method for systematic optimization of neural-network quantum states

Recently, artificial intelligence for science has made significant inroads into various fields of natural science research. In the field of quantum many-body computation, researchers have developed numerous ground state solvers based on neural-network quantum states (NQSs), achieving ground state energies with accuracy comparable to or surpassing traditional methods such as variational Monte Carlo methods, density matrix renormalization group, and quantum Monte Carlo methods. Here, we combine supervised learning, reinforcement learning, and the Lanczos method to develop a systematic approach to improving the NQSs of many-body systems, which we refer to as the NQS Lanczos method. The algorithm mainly consists of two parts: the supervised learning part and the reinforcement learning part. Through supervised learning, the Lanczos states are represented by the NQSs. Through reinforcement learning, the NQSs are further optimized. We analyze the reasons for the underfitting problem and demonstrate how the NQS Lanczos method systematically improves the energy in the highly frustrated regime of the two-dimensional Heisenberg $J_1$-$J_2$ model. Compared to the existing method that combines the Lanczos method with the restricted Boltzmann machine, the primary advantage of the NQS Lanczos method is its linearly increasing computational cost.

Variational optimization of the amplitude of neural-network quantum many-body ground states

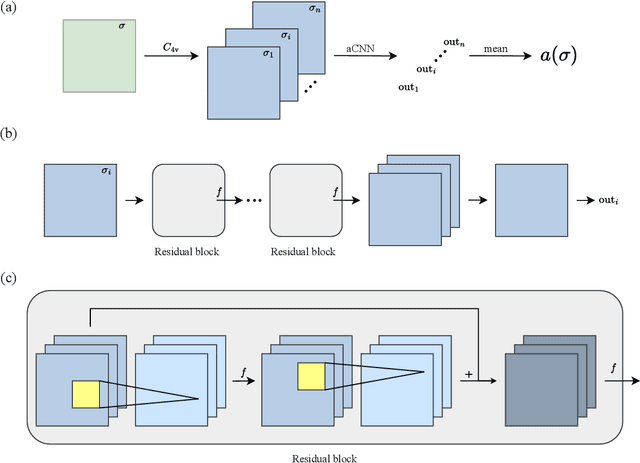
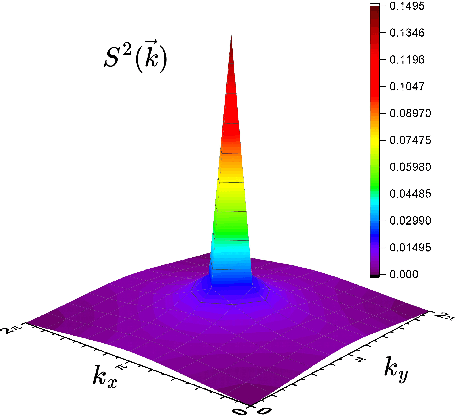
Neural-network quantum states (NQSs), variationally optimized by combining traditional methods and deep learning techniques, is a new way to find quantum many-body ground states and gradually becomes a competitor of traditional variational methods. However, there are still some difficulties in the optimization of NQSs, such as local minima, slow convergence, and sign structure optimization. Here, we split a quantum many-body variational wave function into a multiplication of a real-valued amplitude neural network and a sign structure, and focus on the optimization of the amplitude network while keeping the sign structure fixed. The amplitude network is a convolutional neural network (CNN) with residual blocks, namely a ResNet. Our method is tested on three typical quantum many-body systems. The obtained ground state energies are lower than or comparable to those from traditional variational Monte Carlo (VMC) methods and density matrix renormalization group (DMRG). Surprisingly, for the frustrated Heisenberg $J_1$-$J_2$ model, our results are better than those of the complex-valued CNN in the literature, implying that the sign structure of the complex-valued NQS is difficult to be optimized. We will study the optimization of the sign structure of NQSs in the future.

A simple framework for contrastive learning phases of matter

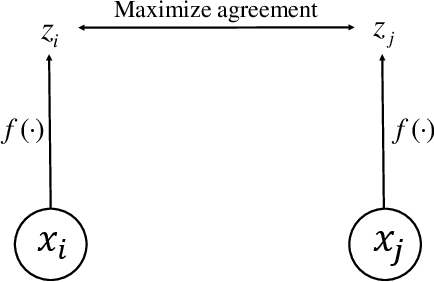
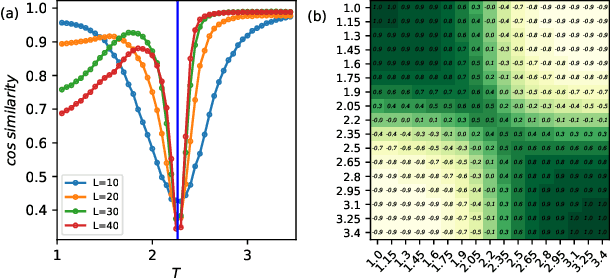
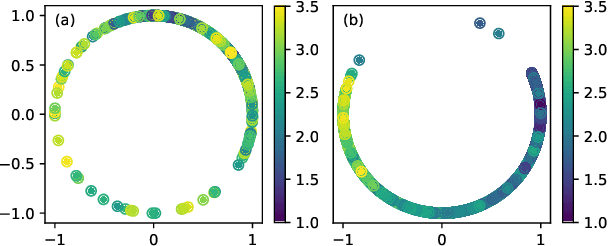
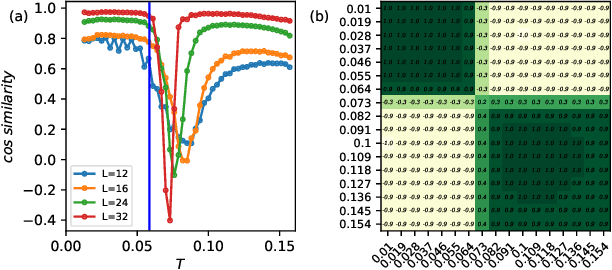
A main task in condensed-matter physics is to recognize, classify, and characterize phases of matter and the corresponding phase transitions, for which machine learning provides a new class of research tools due to the remarkable development in computing power and algorithms. Despite much exploration in this new field, usually different methods and techniques are needed for different scenarios. Here, we present SimCLP: a simple framework for contrastive learning phases of matter, which is inspired by the recent development in contrastive learning of visual representations. We demonstrate the success of this framework on several representative systems, including classical and quantum, single-particle and many-body, conventional and topological. SimCLP is flexible and free of usual burdens such as manual feature engineering and prior knowledge. The only prerequisite is to prepare enough state configurations. Furthermore, it can generate representation vectors and labels and hence help tackle other problems. SimCLP therefore paves an alternative way to the development of a generic tool for identifying unexplored phase transitions.

Compressing deep neural networks by matrix product operators

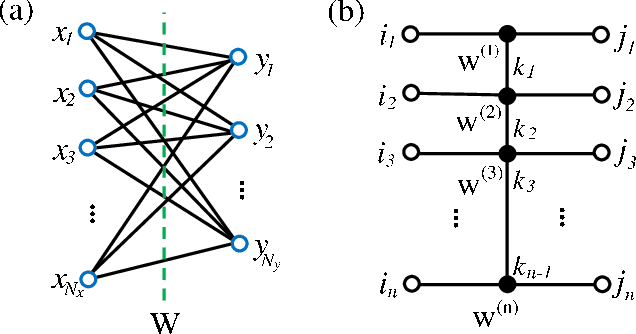
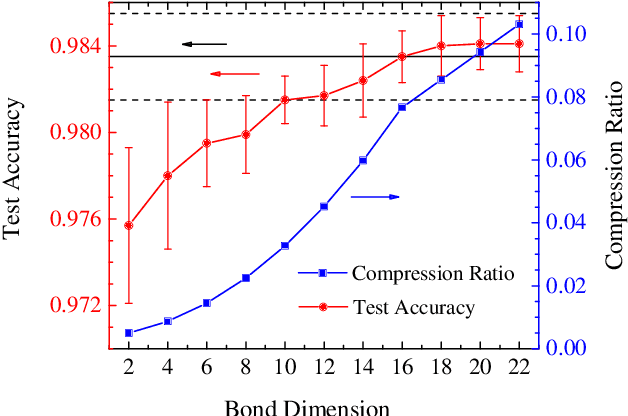
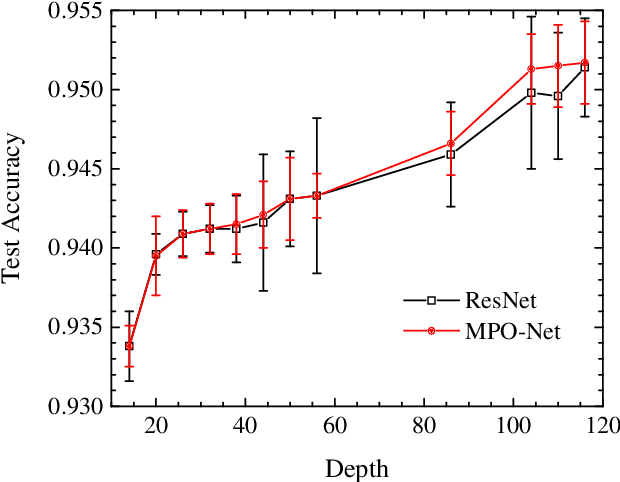
A deep neural network is a parameterization of a multi-layer mapping of signals in terms of many alternatively arranged linear and nonlinear transformations. The linear transformations, which are generally used in the fully-connected as well as convolutional layers, contain most of the variational parameters that are trained and stored. Compressing a deep neural network to reduce its number of variational parameters but not its prediction power is an important but challenging problem towards the establishment of an optimized scheme in training efficiently these parameters and in lowering the risk of overfitting. Here we show that this problem can be effectively solved by representing linear transformations with matrix product operators (MPO). We have tested this approach in five main neural networks, including FC2, LeNet-5, VGG, ResNet, and DenseNet on two widely used datasets, namely MNIST and CIFAR-10, and found that this MPO representation indeed sets up a faithful and efficient mapping between input and output signals, which can keep or even improve the prediction accuracy with dramatically reduced number of parameters.