Variational optimization of the amplitude of neural-network quantum many-body ground states
Paper and Code
Aug 18, 2023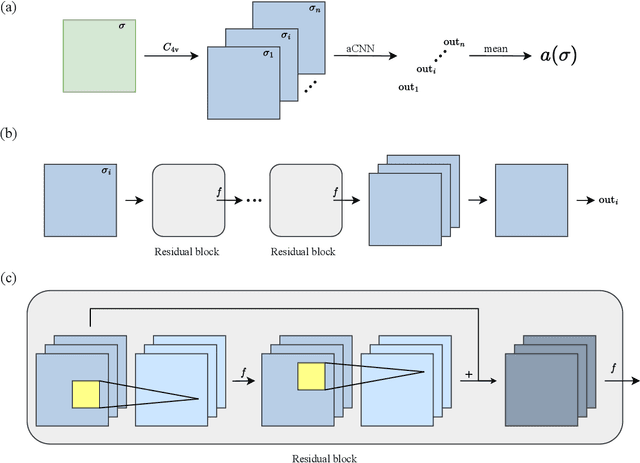
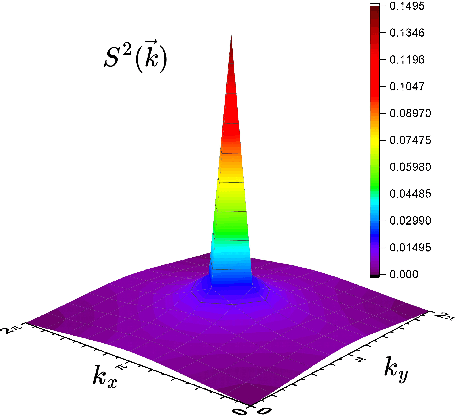


Neural-network quantum states (NQSs), variationally optimized by combining traditional methods and deep learning techniques, is a new way to find quantum many-body ground states and gradually becomes a competitor of traditional variational methods. However, there are still some difficulties in the optimization of NQSs, such as local minima, slow convergence, and sign structure optimization. Here, we split a quantum many-body variational wave function into a multiplication of a real-valued amplitude neural network and a sign structure, and focus on the optimization of the amplitude network while keeping the sign structure fixed. The amplitude network is a convolutional neural network (CNN) with residual blocks, namely a ResNet. Our method is tested on three typical quantum many-body systems. The obtained ground state energies are lower than or comparable to those from traditional variational Monte Carlo (VMC) methods and density matrix renormalization group (DMRG). Surprisingly, for the frustrated Heisenberg $J_1$-$J_2$ model, our results are better than those of the complex-valued CNN in the literature, implying that the sign structure of the complex-valued NQS is difficult to be optimized. We will study the optimization of the sign structure of NQSs in the future.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge