Zhong-Yi Lu
PhononBench:A Large-Scale Phonon-Based Benchmark for Dynamical Stability in Crystal Generation
Dec 24, 2025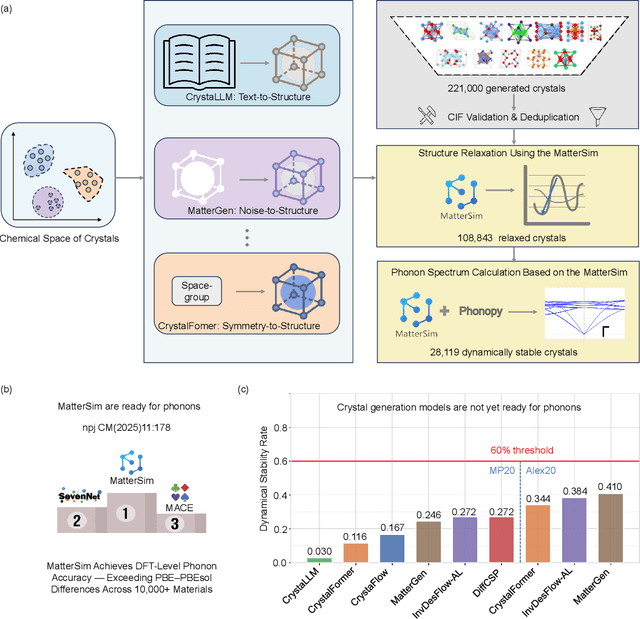
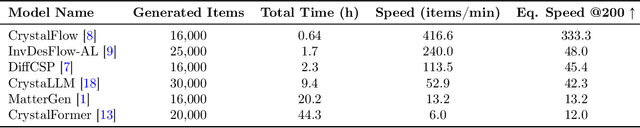
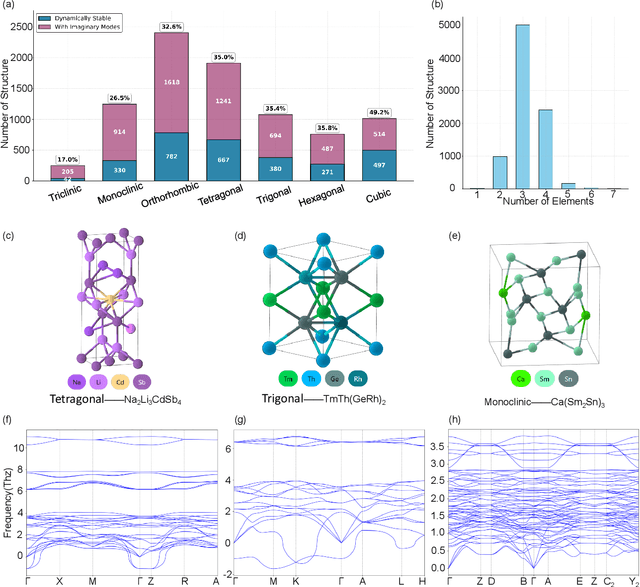
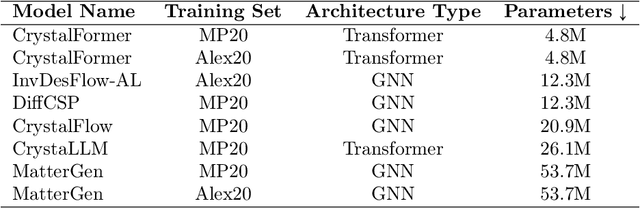
Abstract:In this work, we introduce PhononBench, the first large-scale benchmark for dynamical stability in AI-generated crystals. Leveraging the recently developed MatterSim interatomic potential, which achieves DFT-level accuracy in phonon predictions across more than 10,000 materials, PhononBench enables efficient large-scale phonon calculations and dynamical-stability analysis for 108,843 crystal structures generated by six leading crystal generation models. PhononBench reveals a widespread limitation of current generative models in ensuring dynamical stability: the average dynamical-stability rate across all generated structures is only 25.83%, with the top-performing model, MatterGen, reaching just 41.0%. Further case studies show that in property-targeted generation-illustrated here by band-gap conditioning with MatterGen--the dynamical-stability rate remains as low as 23.5% even at the optimal band-gap condition of 0.5 eV. In space-group-controlled generation, higher-symmetry crystals exhibit better stability (e.g., cubic systems achieve rates up to 49.2%), yet the average stability across all controlled generations is still only 34.4%. An important additional outcome of this study is the identification of 28,119 crystal structures that are phonon-stable across the entire Brillouin zone, providing a substantial pool of reliable candidates for future materials exploration. By establishing the first large-scale dynamical-stability benchmark, this work systematically highlights the current limitations of crystal generation models and offers essential evaluation criteria and guidance for their future development toward the design and discovery of physically viable materials. All model-generated crystal structures, phonon calculation results, and the high-throughput evaluation workflows developed in PhononBench will be openly released at https://github.com/xqh19970407/PhononBench
HTSC-2025: A Benchmark Dataset of Ambient-Pressure High-Temperature Superconductors for AI-Driven Critical Temperature Prediction
Jun 04, 2025Abstract:The discovery of high-temperature superconducting materials holds great significance for human industry and daily life. In recent years, research on predicting superconducting transition temperatures using artificial intelligence~(AI) has gained popularity, with most of these tools claiming to achieve remarkable accuracy. However, the lack of widely accepted benchmark datasets in this field has severely hindered fair comparisons between different AI algorithms and impeded further advancement of these methods. In this work, we present the HTSC-2025, an ambient-pressure high-temperature superconducting benchmark dataset. This comprehensive compilation encompasses theoretically predicted superconducting materials discovered by theoretical physicists from 2023 to 2025 based on BCS superconductivity theory, including the renowned X$_2$YH$_6$ system, perovskite MXH$_3$ system, M$_3$XH$_8$ system, cage-like BCN-doped metal atomic systems derived from LaH$_{10}$ structural evolution, and two-dimensional honeycomb-structured systems evolving from MgB$_2$. The HTSC-2025 benchmark has been open-sourced at https://github.com/xqh19970407/HTSC-2025 and will be continuously updated. This benchmark holds significant importance for accelerating the discovery of superconducting materials using AI-based methods.
InvDesFlow-AL: Active Learning-based Workflow for Inverse Design of Functional Materials
May 14, 2025Abstract:Developing inverse design methods for functional materials with specific properties is critical to advancing fields like renewable energy, catalysis, energy storage, and carbon capture. Generative models based on diffusion principles can directly produce new materials that meet performance constraints, thereby significantly accelerating the material design process. However, existing methods for generating and predicting crystal structures often remain limited by low success rates. In this work, we propose a novel inverse material design generative framework called InvDesFlow-AL, which is based on active learning strategies. This framework can iteratively optimize the material generation process to gradually guide it towards desired performance characteristics. In terms of crystal structure prediction, the InvDesFlow-AL model achieves an RMSE of 0.0423 {\AA}, representing an 32.96% improvement in performance compared to exsisting generative models. Additionally, InvDesFlow-AL has been successfully validated in the design of low-formation-energy and low-Ehull materials. It can systematically generate materials with progressively lower formation energies while continuously expanding the exploration across diverse chemical spaces. These results fully demonstrate the effectiveness of the proposed active learning-driven generative model in accelerating material discovery and inverse design. To further prove the effectiveness of this method, we took the search for BCS superconductors under ambient pressure as an example explored by InvDesFlow-AL. As a result, we successfully identified Li\(_2\)AuH\(_6\) as a conventional BCS superconductor with an ultra-high transition temperature of 140 K. This discovery provides strong empirical support for the application of inverse design in materials science.
Generalized Lanczos method for systematic optimization of neural-network quantum states
Feb 03, 2025Abstract:Recently, artificial intelligence for science has made significant inroads into various fields of natural science research. In the field of quantum many-body computation, researchers have developed numerous ground state solvers based on neural-network quantum states (NQSs), achieving ground state energies with accuracy comparable to or surpassing traditional methods such as variational Monte Carlo methods, density matrix renormalization group, and quantum Monte Carlo methods. Here, we combine supervised learning, reinforcement learning, and the Lanczos method to develop a systematic approach to improving the NQSs of many-body systems, which we refer to as the NQS Lanczos method. The algorithm mainly consists of two parts: the supervised learning part and the reinforcement learning part. Through supervised learning, the Lanczos states are represented by the NQSs. Through reinforcement learning, the NQSs are further optimized. We analyze the reasons for the underfitting problem and demonstrate how the NQS Lanczos method systematically improves the energy in the highly frustrated regime of the two-dimensional Heisenberg $J_1$-$J_2$ model. Compared to the existing method that combines the Lanczos method with the restricted Boltzmann machine, the primary advantage of the NQS Lanczos method is its linearly increasing computational cost.
Strong phonon-mediated high temperature superconductivity in Li$_2$AuH$_6$ under ambient pressure
Jan 21, 2025



Abstract:We used our developed AI search engine~(InvDesFlow) to perform extensive investigations regarding ambient stable superconducting hydrides. A cubic structure Li$_2$AuH$_6$ with Au-H octahedral motifs is identified to be a candidate. After performing thermodynamical analysis, we provide a feasible route to experimentally synthesize this material via the known LiAu and LiH compounds under ambient pressure. The further first-principles calculations suggest that Li$_2$AuH$_6$ shows a high superconducting transition temperature ($T_c$) $\sim$ 140 K under ambient pressure. The H-1$s$ electrons strongly couple with phonon modes of vibrations of Au-H octahedrons as well as vibrations of Li atoms, where the latter is not taken seriously in other previously similar cases. Hence, different from previous claims of searching metallic covalent bonds to find high-$T_c$ superconductors, we emphasize here the importance of those phonon modes with strong electron-phonon coupling (EPC). And we suggest that one can intercalate atoms into binary or ternary hydrides to introduce more potential phonon modes with strong EPC, which is an effective approach to find high-$T_c$ superconductors within multicomponent compounds.
AI-driven inverse design of materials: Past, present and future
Nov 14, 2024



Abstract:The discovery of advanced materials is the cornerstone of human technological development and progress. The structures of materials and their corresponding properties are essentially the result of a complex interplay of multiple degrees of freedom such as lattice, charge, spin, symmetry, and topology. This poses significant challenges for the inverse design methods of materials. Humans have long explored new materials through a large number of experiments and proposed corresponding theoretical systems to predict new material properties and structures. With the improvement of computational power, researchers have gradually developed various electronic structure calculation methods, particularly such as the one based density functional theory, as well as high-throughput computational methods. Recently, the rapid development of artificial intelligence technology in the field of computer science has enabled the effective characterization of the implicit association between material properties and structures, thus opening up an efficient paradigm for the inverse design of functional materials. A significant progress has been made in inverse design of materials based on generative and discriminative models, attracting widespread attention from researchers. Considering this rapid technological progress, in this survey, we look back on the latest advancements in AI-driven inverse design of materials by introducing the background, key findings, and mainstream technological development routes. In addition, we summarize the remaining issues for future directions. This survey provides the latest overview of AI-driven inverse design of materials, which can serve as a useful resource for researchers.
Over-parameterized Student Model via Tensor Decomposition Boosted Knowledge Distillation
Nov 10, 2024



Abstract:Increased training parameters have enabled large pre-trained models to excel in various downstream tasks. Nevertheless, the extensive computational requirements associated with these models hinder their widespread adoption within the community. We focus on Knowledge Distillation (KD), where a compact student model is trained to mimic a larger teacher model, facilitating the transfer of knowledge of large models. In contrast to much of the previous work, we scale up the parameters of the student model during training, to benefit from overparameterization without increasing the inference latency. In particular, we propose a tensor decomposition strategy that effectively over-parameterizes the relatively small student model through an efficient and nearly lossless decomposition of its parameter matrices into higher-dimensional tensors. To ensure efficiency, we further introduce a tensor constraint loss to align the high-dimensional tensors between the student and teacher models. Comprehensive experiments validate the significant performance enhancement by our approach in various KD tasks, covering computer vision and natural language processing areas. Our code is available at https://github.com/intell-sci-comput/OPDF.
AI-accelerated discovery of high critical temperature superconductors
Sep 12, 2024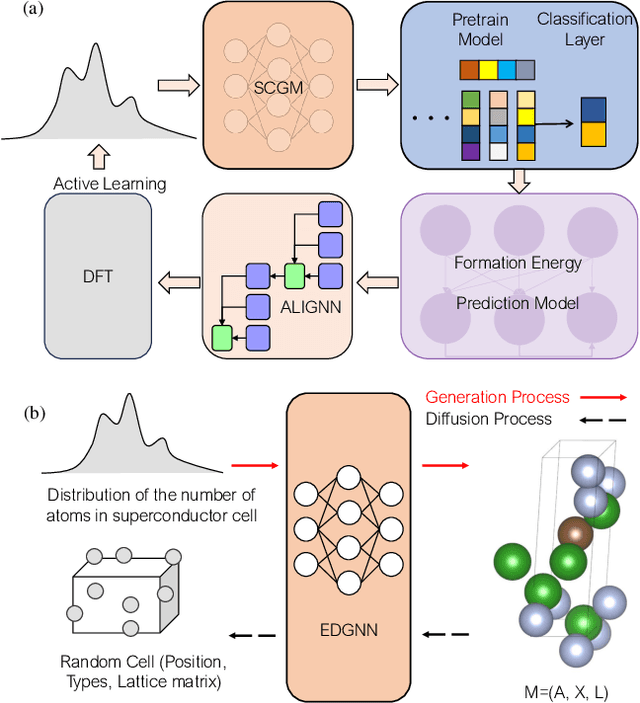
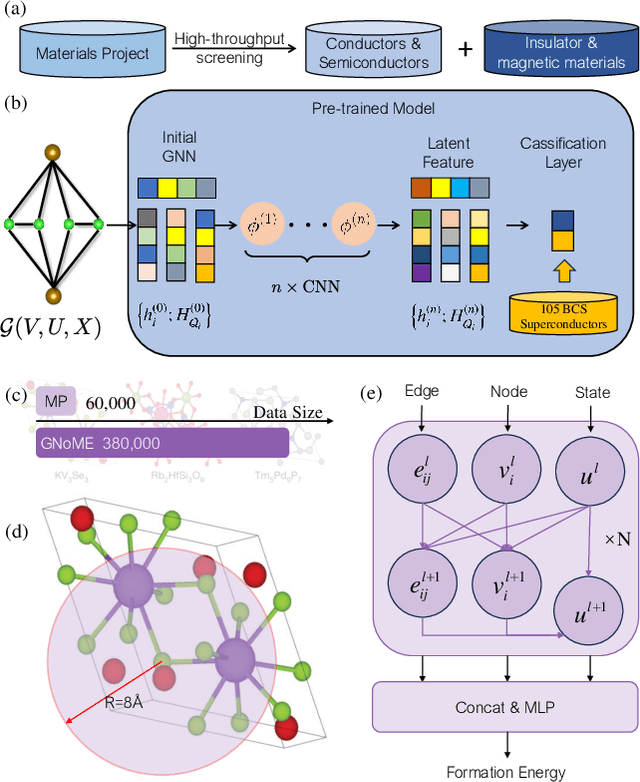
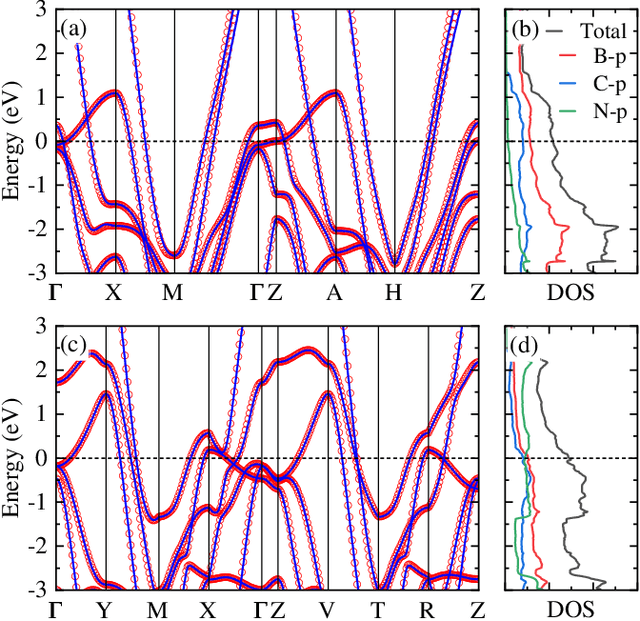
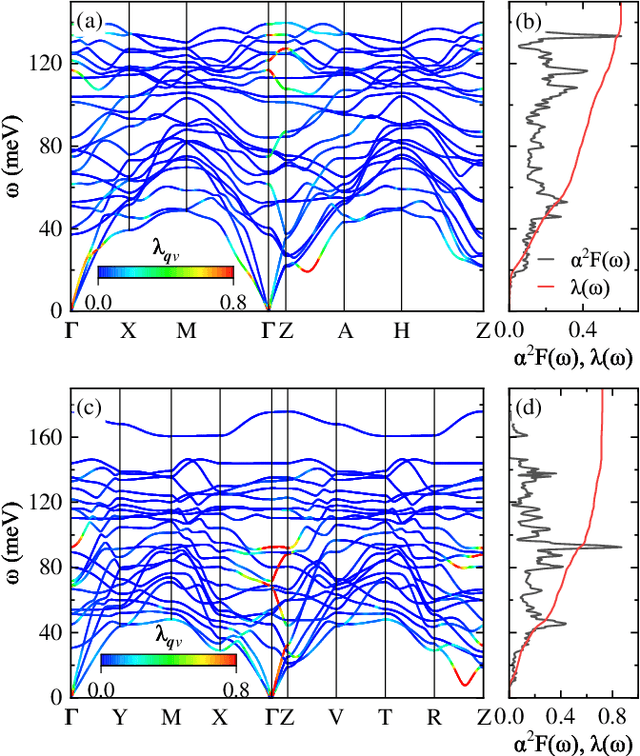
Abstract:The discovery of new superconducting materials, particularly those exhibiting high critical temperature ($T_c$), has been a vibrant area of study within the field of condensed matter physics. Conventional approaches primarily rely on physical intuition to search for potential superconductors within the existing databases. However, the known materials only scratch the surface of the extensive array of possibilities within the realm of materials. Here, we develop an AI search engine that integrates deep model pre-training and fine-tuning techniques, diffusion models, and physics-based approaches (e.g., first-principles electronic structure calculation) for discovery of high-$T_c$ superconductors. Utilizing this AI search engine, we have obtained 74 dynamically stable materials with critical temperatures predicted by the AI model to be $T_c \geq$ 15 K based on a very small set of samples. Notably, these materials are not contained in any existing dataset. Furthermore, we analyze trends in our dataset and individual materials including B$_4$CN$_3$ and B$_5$CN$_2$ whose $T_c$s are 24.08 K and 15.93 K, respectively. We demonstrate that AI technique can discover a set of new high-$T_c$ superconductors, outline its potential for accelerating discovery of the materials with targeted properties.
AI-accelerated Discovery of Altermagnetic Materials
Nov 13, 2023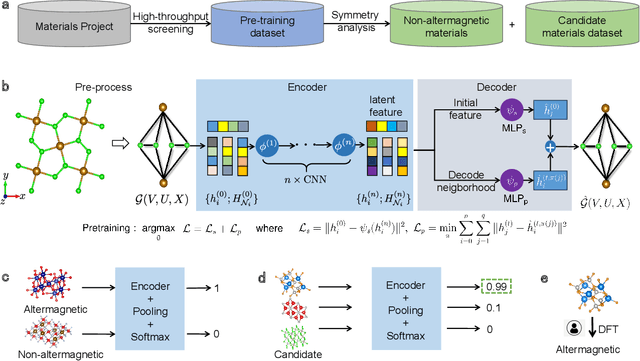
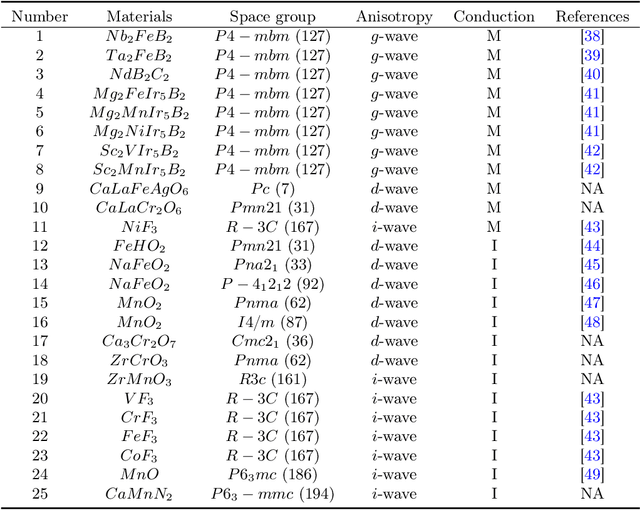
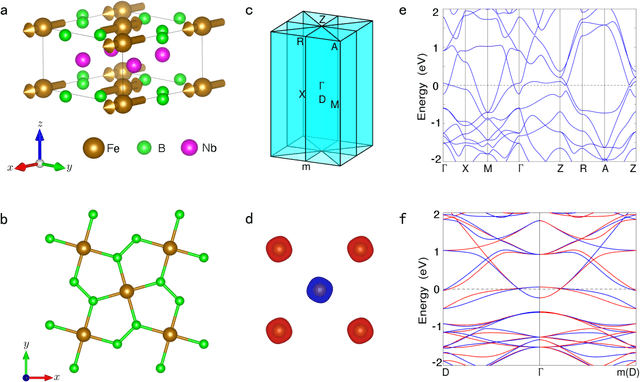
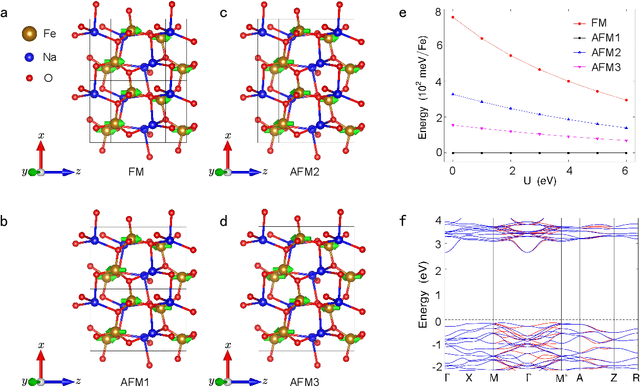
Abstract:Altermagnetism, a new magnetic phase, has been theoretically proposed and experimentally verified to be distinct from ferromagnetism and antiferromagnetism. Although altermagnets have been found to possess many exotic physical properties, the very limited availability of known altermagnetic materials (e.g., 14 confirmed materials) hinders the study of such properties. Hence, discovering more types of altermagnetic materials is crucial for a comprehensive understanding of altermagnetism and thus facilitating new applications in the next-generation information technologies, e.g., storage devices and high-sensitivity sensors. Here, we report 25 new altermagnetic materials that cover metals, semiconductors, and insulators, discovered by an AI search engine unifying symmetry analysis, graph neural network pre-training, optimal transport theory, and first-principles electronic structure calculation. The wide range of electronic structural characteristics reveals that various novel physical properties manifest in these newly discovered altermagnetic materials, e.g., anomalous Hall effect, anomalous Kerr effect, and topological property. Noteworthy, we discovered 8 i-wave altermagnetic materials for the first time. Overall, the AI search engine performs much better than human experts and suggests a set of new altermagnetic materials with unique properties, outlining its potential for accelerated discovery of the materials with targeting properties.
Variational optimization of the amplitude of neural-network quantum many-body ground states
Aug 18, 2023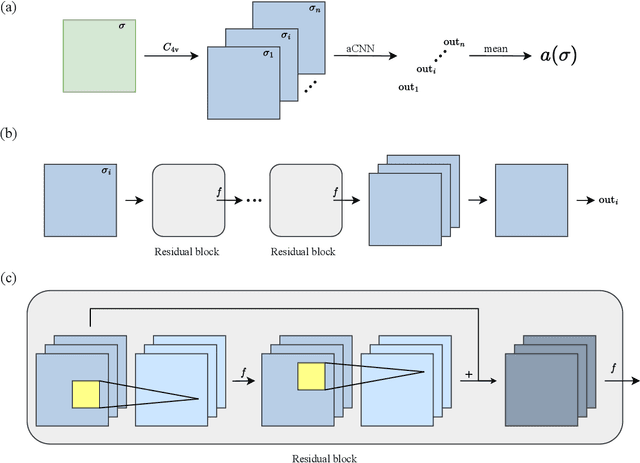
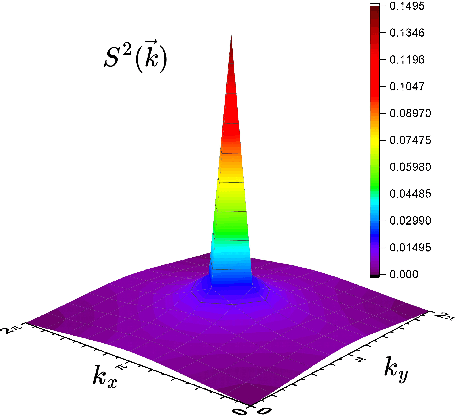


Abstract:Neural-network quantum states (NQSs), variationally optimized by combining traditional methods and deep learning techniques, is a new way to find quantum many-body ground states and gradually becomes a competitor of traditional variational methods. However, there are still some difficulties in the optimization of NQSs, such as local minima, slow convergence, and sign structure optimization. Here, we split a quantum many-body variational wave function into a multiplication of a real-valued amplitude neural network and a sign structure, and focus on the optimization of the amplitude network while keeping the sign structure fixed. The amplitude network is a convolutional neural network (CNN) with residual blocks, namely a ResNet. Our method is tested on three typical quantum many-body systems. The obtained ground state energies are lower than or comparable to those from traditional variational Monte Carlo (VMC) methods and density matrix renormalization group (DMRG). Surprisingly, for the frustrated Heisenberg $J_1$-$J_2$ model, our results are better than those of the complex-valued CNN in the literature, implying that the sign structure of the complex-valued NQS is difficult to be optimized. We will study the optimization of the sign structure of NQSs in the future.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge